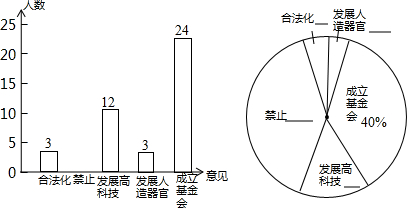
题目内容
14.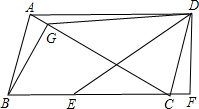 在平行四边形ABCD中,CA=CB=AD,过B作BG⊥AC于G,过D作DF⊥BC于F,且BC上一点E满足DE=DG;
在平行四边形ABCD中,CA=CB=AD,过B作BG⊥AC于G,过D作DF⊥BC于F,且BC上一点E满足DE=DG;(1)求证:AG=CF;
(2)求证:CG=EF+CF.
分析 (1)根据平行四边形的性质得出AB=CD,AB∥CD,根据平行线性质,等腰三角形性质和已知推出∠1=∠3,求出∠BGA=∠F=90°,根据AAS推出△ABG≌△CDF即可;
(2)在CG上截取CH,使CH=CF,连结DH,根据全等三角形的判定证出△DCH≌△DCF,根据全等三角形的性质推出DH=DF,根据全等三角形的判定得出Rt△DHG≌Rt△DFE,推出EF=HG,即可得出答案.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABC=∠3,
∵AC=BC,
∴∠1=∠ABC,
∴∠1=∠3,
∵BG⊥AC,DF⊥BC,
∴∠BGA=∠F=90°,
在△ABG和△CDF中
$\left\{\begin{array}{l}{∠BGA=∠F}\\{∠1=∠3}\\{AB=CD}\end{array}\right.$
∴△ABG≌△CDF(AAS),
∴AG=CF;
(2)在CG上截取CH,使CH=CF,连结DH,
∵AB∥CD,
∴∠1=∠2,∠ABC=∠3,
∵AC=BC,
∴∠1=∠ABC,
∴∠2=∠3,
在△DCH和△DCF中,
$\left\{\begin{array}{l}{DC=DC}\\{∠2=∠3}\\{CH=CF}\end{array}\right.$
∴△DCH≌△DCF(SAS),
∴DH=DF,
∵∠F=∠DHG=90°,
∴在Rt△DHG和Rt△DFE中,
$\left\{\begin{array}{l}{DG=DE}\\{DH=DF}\end{array}\right.$,
∴Rt△DHG≌Rt△DFE(HL),
∴EF=HG,
∵CF=CH,
∴CG=GH+CH=EF+CF.
点评 本题考查了等腰三角形的性质,平行线的性质,平行四边形的性质,全等三角形的性质和判定的应用,能正确运用定理进行推理是解此题的关键,综合性比较强,难度偏大.

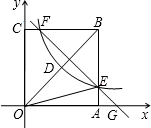 如图,正方形OABC的边OA、OC均在坐标轴上,双曲线y=$\frac{k}{x}$(x>0)经过OB的中点D,与AB边交于点E,与CB边交于点F,直线EF与x轴交于G. 若S△OAE=4.5,则点G的坐标是( )
如图,正方形OABC的边OA、OC均在坐标轴上,双曲线y=$\frac{k}{x}$(x>0)经过OB的中点D,与AB边交于点E,与CB边交于点F,直线EF与x轴交于G. 若S△OAE=4.5,则点G的坐标是( )| A. | (7,0) | B. | (7.5,0) | C. | (8,0) | D. | (8.5,0) |
| A. |  | B. |  | C. |  | D. |  |
| A. | m<-1 | B. | m>-1 | C. | m=1 | D. | m<0 |
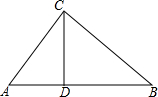 △ABC中,AB=17,AC=10,AB边上的高CD=8,求BC的长.
△ABC中,AB=17,AC=10,AB边上的高CD=8,求BC的长.