题目内容
16.△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是234或126.分析 分三角形ABC为锐角三角形、三角形ABC为钝角三角形两种情况,根据AH垂直于BC,利用垂直的定义得到三角形ABH与三角形AHC为直角三角形,利用勾股定理分别求出BH与HC,由BH+HC=BC或BH-HC=BC求出BC,利用三角形的面积公式即可求出三角形ABC的面积.
解答 解:①当△ABC为锐角三角形时,如图1所示,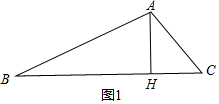
∵AH⊥BC,
∴∠AHB=∠AHC=90°,
在Rt△ABH中,AB=41,AH=9,
根据勾股定理得:BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=40,
在Rt△AHC中,AC=15,AH=9,
根据勾股定理得:HC=$\sqrt{A{C}^{2}-A{H}^{2}}$=12,
∴BC=BH+HC=40+12=52,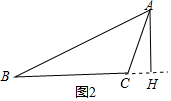
则S△ABC=$\frac{1}{2}$BC•AH=234;
②当△ABC为钝角三角形时,如图2所示,
由①得,BH=40,CH=12,
∴BC=BH-HC=40-12=28,
则S△ABC=$\frac{1}{2}$BC•AH=126.
综上,△ABC的面积为234或126.
故答案为:234或126.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
相关题目
6.方程3x2-x+1=0的二次项系数和一次项系数分别为( )
| A. | 3和0 | B. | 3和-1 | C. | 2和-1 | D. | 3和1 |
4.下列不能用平方差公式计算的是( )
| A. | (-5-a)(a-5) | B. | (-2a+3b)(3b+2a) | C. | (a+b+c)(a-b+c) | D. | (a-b-c)(-a+b+c) |
5.下列关于x的方程有实数根的是( )
| A. | x2-x+1=0 | B. | x2+x+1=0 | C. | (x-1)2+1=0 | D. | (x-1)(x+2)=0 |
 如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.
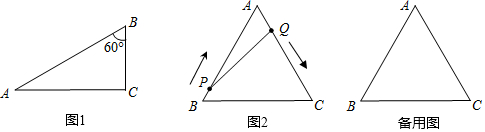
如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.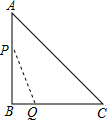 如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$.
如图,在△ABC中,∠B=90°,AB=BC=4,动点P从点A出发沿A→B→C运动,动点Q从点B出发沿B→C→A运动.如果P、Q两点同时出发,速度均为1个单位/秒.设出发时间为x秒(0≤x≤8),记△PBQ的面积y1的函数图象为T.若直线y2=x+b与T只有一个交点,则b的取值范围为b=-$\frac{9\sqrt{2}}{2}$或4$\sqrt{2}$-8<b<0或b=$\frac{1}{2}$. 如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )