题目内容
6. 如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )| A. | 2π-4 | B. | 4π-8 | C. | 2π-8 | D. | 4π-4 |
分析 连接OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积-△ODC的面积,依此列式计算即可求解.
解答 解:连接OC,如图所示: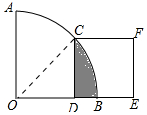
∵在扇形AOB中∠AOB=90°,$\widehat{AC}$=$\widehat{BC}$,
∴∠COD=45°,
∴OD=CD,
∴OC=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,
∴阴影部分的面积=扇形BOC的面积-△ODC的面积
=$\frac{45π×{4}^{2}}{360}$-$\frac{1}{2}$×(2$\sqrt{2}$)2=2π-4.
故选:A.
点评 此题考查了正方形的性质和扇形面积的计算,解题的关键是得到扇形半径的长度.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
1.若m<0,n>0,则一次函数y=mx-n的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.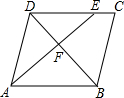 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )| A. | 3:4 | B. | 9:16 | C. | 4:9 | D. | 1:3 |
15.不等式2x-8<0的正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.为增强居民节约用水意识,深圳市在2011年开始对供水范围内的居民用水实行“阶梯收费”,具体收费标准如下表:
某户居民四月份用水10米3时,缴纳水费23元.
(1)求a的值;
(2)若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.
| 一户居民一个月用水量即为x米3 | 水费单价 (单位:元/米3) |
| x≤22 | a |
| 超出22米3的部分 | a+1.1 |
(1)求a的值;
(2)若该户居民五月份所缴水费为71元,求该户居民五月份的用水量.