题目内容
小明动手做了一个质地均匀、六个面完全相同的正方形,分别标有整数-2、-1、0、1、2、3,且每个面和它所对的面的数字之和均相等,小明向上抛掷该正方体,落地后正方体正面朝上数字作为点P的横坐标,将它所对的面的数字作为点P的纵坐标,则点P落在抛物线y=-
x2+6与x轴所围成的区域内(不含边界)的概率是 .
| 1 |
| 2 |
考点:列表法与树状图法,二次函数的性质
专题:
分析:由条件分析可以得出P点的坐标共有6中情况:(-1,2)、(-2,3)、(0,1)、(2,-1)、(1,0)、(3,-2),在求出抛物线y=-
x2+6与x轴所围成的区域内(不含边界)的是有可能情况,即可得到P落在抛物线内的概率.
| 1 |
| 2 |
解答:解:∵正方体骰子(每个面的点数分别为-2、-1、0、1、2、3,且相对面的点数和相等,
∴P点的坐标为::(-1,2)、(-2,3)、(0,1)、(2,-1)、(1,0)、(3,-2),
∵y=-
x2+6,
令y=0,则x=-2
或2
∴与x轴所围成的区域内(不含边界)取值范围为:-2
<x<2
,
∴点P落在抛物线y=-
x2+6与x轴所围成的区域内(不含边界)有(-1,2)、(-2,0)、(0,1)、(0,1),
点P落在抛物线y=-
x2+6与x轴所围成的区域内(不含边界)的概率=
.
∴P点的坐标为::(-1,2)、(-2,3)、(0,1)、(2,-1)、(1,0)、(3,-2),
∵y=-
| 1 |
| 2 |
令y=0,则x=-2
| 3 |
| 3 |
∴与x轴所围成的区域内(不含边界)取值范围为:-2
| 3 |
| 3 |
∴点P落在抛物线y=-
| 1 |
| 2 |
点P落在抛物线y=-
| 1 |
| 2 |
| 2 |
| 3 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知y=
,如果用y的代数式表示x,那么x=( )
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
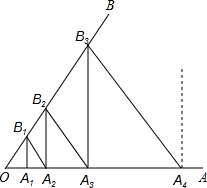 如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是
如图,已知∠AOB=60°,在OA上取OA1=1,过点A1作A1B1⊥OA交OB于点B1,过点B1作B1A2⊥OB交OA于点A2,过点A2作A2B2⊥OA交OB于点B2,过点B2作B2A3⊥OB交OA于点A3,…,按此作法继续下去,则OA10的值是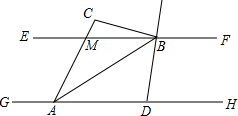 如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为
如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为