题目内容
已知一个五位数
满足三个条件:①它的各位数字均不相同且不为零;②它是一个完全平方数;③它的万位上的数字a是一个完全平方数,千位和百位上的数字顺次构成的两位数
以及十位和个位上的数字顺次构成的两位数
也都是完全平方数.那么满足上述条件的五位数是 .
. |
| abcde |
. |
| bc |
. |
| de |
考点:完全平方数
专题:
分析:首先设M2=
,且a=m2(一位数),
=n 2(两位数),
=t2(两位数),则M2=m2×104+n2×102+t2①,又由M2=(m×102+t)2=m2×104+2mt×102+t2②,可求得n2=2mt.继而可分析求得n2的值,继而求得答案.
. |
| abcde |
. |
| bc |
. |
| de |
解答:解:设M2=
,且a=m2(一位数),
=n 2(两位数),
=t2(两位数),
则M2=m2×104+n2×102+t2①,
∵它是一个完全平方数,
∴由式①知:M2=(m×102+t)2=m2×104+2mt×102+t2②
比较式①、式②得:n2=2mt.
∵n2是2的倍数,
∴n也是2的倍数,
∴n2是4的倍数,且是完全平方数.
故n2=16或36或64.
当n2=16时,得mt=8,则m=l,2,4,8,t=8,4,2,1,
∵它的各位数字均不相同且不为零,
∴都不合条件,舍去.
当n2=36时,得mt=18.则m=2,3,1,t=9,6,18.
∵它的各位数字均不相同且不为零,
∴M2=43681.
当n2=64时,得mt=32.则m=1,2,4,8,t=32,16,8,4,
它的各位数字均不相同且不为零,
∴都不合条件,舍去.
满足条件的五位数为43681.
故答案为:43681.
. |
| abcde |
. |
| bc |
. |
| de |
则M2=m2×104+n2×102+t2①,
∵它是一个完全平方数,
∴由式①知:M2=(m×102+t)2=m2×104+2mt×102+t2②
比较式①、式②得:n2=2mt.
∵n2是2的倍数,
∴n也是2的倍数,
∴n2是4的倍数,且是完全平方数.
故n2=16或36或64.
当n2=16时,得mt=8,则m=l,2,4,8,t=8,4,2,1,
∵它的各位数字均不相同且不为零,
∴都不合条件,舍去.
当n2=36时,得mt=18.则m=2,3,1,t=9,6,18.
∵它的各位数字均不相同且不为零,
∴M2=43681.
当n2=64时,得mt=32.则m=1,2,4,8,t=32,16,8,4,
它的各位数字均不相同且不为零,
∴都不合条件,舍去.
满足条件的五位数为43681.
故答案为:43681.
点评:此题考查了完全平方数的知识.此题难度较大,注意设M2=
,且a=m2(一位数),
=n 2(两位数),
=t2(两位数),根据题意求得n2=2mt是解此题的关键.
. |
| abcde |
. |
| bc |
. |
| de |

练习册系列答案
相关题目
已知一个三角形的三边长均为整数,若其中仅有一条边长为5,且它不是最短边,也不是最长边,则满足条件的三角形共有( )
| A、10个 | B、8个 | C、6个 | D、4个 |
在打靶中,某运动员每发子弹都是命中8、9、10环,他打了多于11发子弹,共得100环,那么,他命中10环的次数是( )
| A、0 | B、1 | C、2 | D、不能确定 |
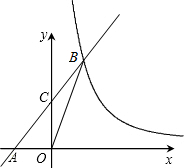 象交于点B(2,n),连接BO,若S△AOB=4.
象交于点B(2,n),连接BO,若S△AOB=4.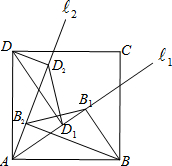 如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由.
如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由. 甲在B地,乙在A地,甲步行,乙骑自行车,他们同时去C地(A、B、C在同一条直线上),下面图象表示他们距A地的路程S(千米)与时间t(小时)之间的函数关系式.结合图象回答下列问题:
甲在B地,乙在A地,甲步行,乙骑自行车,他们同时去C地(A、B、C在同一条直线上),下面图象表示他们距A地的路程S(千米)与时间t(小时)之间的函数关系式.结合图象回答下列问题: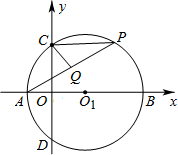 如图,在直角坐标系中,O1(3,0),A(-2,0),以O1为圆心,O1A为半径的⊙O1交y轴于C、D两点,P为弧BC上一点,CQ平分∠DCP,交AP于点Q,则AQ的长为( )
如图,在直角坐标系中,O1(3,0),A(-2,0),以O1为圆心,O1A为半径的⊙O1交y轴于C、D两点,P为弧BC上一点,CQ平分∠DCP,交AP于点Q,则AQ的长为( ) 如图,⊙O 是△ABC 的外接圆,BC=a,CA=b,且∠A-∠B=90°.则⊙O的半径为
如图,⊙O 是△ABC 的外接圆,BC=a,CA=b,且∠A-∠B=90°.则⊙O的半径为