题目内容
如图，有一块直角三角形纸片两直角边AC=5cm，BC=12cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．考点：翻折变换（折叠问题）
专题：
分析：利用翻折变换的性质得出DE=CD，AC=AE=5cm，∠DEB=90°，进而利用勾股定理得出x的值．
解答：解：∵有一块直角三角形纸片两直角边AC=5cm，BC=12cm，
∴AB=13cm，
∵将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，
∴DE=CD，AC=AE=5cm，∠DEB=90°，
设CD=xcm，则BD=（12-x）cm，
故DE2+BE2=BD2，
即x2+（13-5）2=（12-x）2，
解得：x=
，
则CD的长为
cm．
∴AB=13cm，
∵将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，
∴DE=CD，AC=AE=5cm，∠DEB=90°，
设CD=xcm，则BD=（12-x）cm，
故DE2+BE2=BD2，
即x2+（13-5）2=（12-x）2，
解得：x=
| 10 |
| 3 |
则CD的长为
| 10 |
| 3 |
点评：此题主要考查了翻折变换的性质以及勾股定理等知识，表示出BD的长是解题关键．
练习册系列答案
相关题目
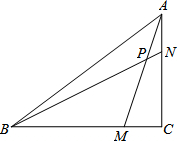如图，△ABC中，∠C=90°，点M在BC上，且BM=AC，点N在AC上，且AN=MC，AM与BN相交于点P，求∠BPM的度数．