题目内容
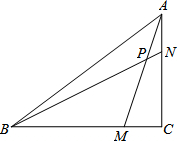 如图,△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,且AN=MC,AM与BN相交于点P,求∠BPM的度数.
如图,△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,且AN=MC,AM与BN相交于点P,求∠BPM的度数.考点:全等三角形的判定与性质,平行四边形的判定与性质
专题:
分析:可过点M作ME∥AN,使ME=AN,连NE,BE,得出四边形AMEN为平行四边形,再通过求证△BEM≌△AMC,可得出△BEN为等腰直角三角形,进而再利用平行线的性质可得出结论.
解答: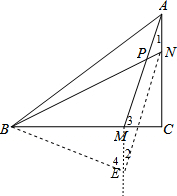 解:如图,过M作ME∥AN,使ME=AN,连NE,BE,
解:如图,过M作ME∥AN,使ME=AN,连NE,BE,
则四边形AMEN为平行四边形,
∴NE=AM,ME⊥BC,
∵AN=MC,
∴ME=CM,
在△BEM和△AMC中,
,
∴△BEM≌△AMC(SAS),
∴BE=AM=NE,∠1=∠2,∠3=∠4,
∵∠1+∠3=90°,
∴∠2+∠4=90°且BE=NE,
∴△BEN为等腰直角三角形,∠BNE=45°,
∵AM∥NE,
∴∠BPM=∠BNE=45°.
 解:如图,过M作ME∥AN,使ME=AN,连NE,BE,
解:如图,过M作ME∥AN,使ME=AN,连NE,BE,则四边形AMEN为平行四边形,
∴NE=AM,ME⊥BC,
∵AN=MC,
∴ME=CM,
在△BEM和△AMC中,
|
∴△BEM≌△AMC(SAS),
∴BE=AM=NE,∠1=∠2,∠3=∠4,
∵∠1+∠3=90°,
∴∠2+∠4=90°且BE=NE,
∴△BEN为等腰直角三角形,∠BNE=45°,
∵AM∥NE,
∴∠BPM=∠BNE=45°.
点评:本题主要考查平行四边形的判定及性质,全等三角形的判定与性质,关键是正确作出辅助线,构造全等三角形和平行四边形.

练习册系列答案
相关题目
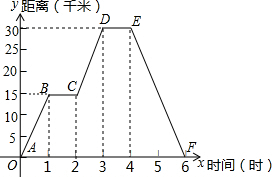 小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
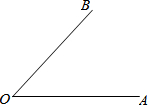 已知∠AOB(如图),求作:
已知∠AOB(如图),求作: 如图,有一块直角三角形纸片两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.