题目内容
已知△AOB和△COD都是等腰直角三角形,AO=BO,CO=DO,△AOB可绕着点O顺时针旋转.

(1)如图1,当点A、O、D在同一直线上时,请指出下列关系:
①AB与CD: ;
②AC与BD: .
(2)若△AOB旋转到图2、图3位置时,上述哪些关系还成立吗?若成立,请选择一个图形给予证明.若都不成立,请说明理由.

(1)如图1,当点A、O、D在同一直线上时,请指出下列关系:
①AB与CD:
②AC与BD:
(2)若△AOB旋转到图2、图3位置时,上述哪些关系还成立吗?若成立,请选择一个图形给予证明.若都不成立,请说明理由.
考点:全等三角形的判定与性质,等腰直角三角形,旋转的性质
专题:
分析:(1)①延长AB交CD于E,根据等腰直角三角形的性质可得∠ABO=45°,∠OCD=45°,再根据三角形内角和定理可得∠CEB=90°,进而得到AB⊥CD;
②证明△AOC≌△BOD可得AC=BD;
(2)AC=BD成立,AB⊥CD不成立;①延长AB、OB交CD于E、F,根据三角形内角与外角的关系可得∠OFD=∠OCD+∠COF>45°,可证明∠AEC≠90°;
②证明△AOC≌△BOD可得AC=BD.
②证明△AOC≌△BOD可得AC=BD;
(2)AC=BD成立,AB⊥CD不成立;①延长AB、OB交CD于E、F,根据三角形内角与外角的关系可得∠OFD=∠OCD+∠COF>45°,可证明∠AEC≠90°;
②证明△AOC≌△BOD可得AC=BD.
解答: 解:(1)AB⊥CD,AC=BD,
解:(1)AB⊥CD,AC=BD,
①延长AB交CD于E,
∵△AOB和△COD都是等腰直角三角形,
∴∠ABO=45°,∠OCD=45°,
∵∠CBE=∠ABO=45°,
∴∠CEB=180°-45°-45°=90°,
∴AB⊥CD;
②∵△AOB和△COD都是等腰直角三角形,
∴∠AOB=∠BOD=90°,
在△AOC和△BOD中
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)AC=BD成立,AB⊥CD不成立,
①延长AB、OB交CD于E、F,
∵△AOB和△COD都是等腰直角三角形,
∴∠ABO=45°,∠OCD=45°,
∴∠FBE=∠ABO=45°,
∵∠OFD=∠OCD+∠COF>45°,
∴∠AEC=180°-45°-∠OFD≠90°,
∴AB⊥CD不成立;
②∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD.
∵△OAB与△COD均为等腰三角形,
∴OA=OB,OC=OD.
在△AOC和△BOD中
,
∴△AOC≌△BOD(SAS),
∴AC=BD.
 解:(1)AB⊥CD,AC=BD,
解:(1)AB⊥CD,AC=BD,①延长AB交CD于E,
∵△AOB和△COD都是等腰直角三角形,
∴∠ABO=45°,∠OCD=45°,
∵∠CBE=∠ABO=45°,
∴∠CEB=180°-45°-45°=90°,
∴AB⊥CD;
②∵△AOB和△COD都是等腰直角三角形,
∴∠AOB=∠BOD=90°,
在△AOC和△BOD中
|
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)AC=BD成立,AB⊥CD不成立,
①延长AB、OB交CD于E、F,
∵△AOB和△COD都是等腰直角三角形,
∴∠ABO=45°,∠OCD=45°,
∴∠FBE=∠ABO=45°,
∵∠OFD=∠OCD+∠COF>45°,
∴∠AEC=180°-45°-∠OFD≠90°,
∴AB⊥CD不成立;
②∵∠AOB=∠COD=90°,

∴∠AOC=∠BOD.
∵△OAB与△COD均为等腰三角形,
∴OA=OB,OC=OD.
在△AOC和△BOD中
|
∴△AOC≌△BOD(SAS),
∴AC=BD.
点评:此题主要考查了全等三角形的判定与性质,以及等腰直角三角形的性质,关键是掌握全等三角形的判定方法.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
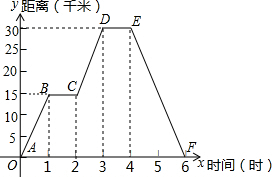 小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
小明同学骑自行车去郊外春游,如图为表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.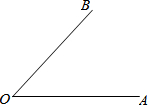 已知∠AOB(如图),求作:
已知∠AOB(如图),求作: 如图,有一块直角三角形纸片两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.