题目内容
9.为响应政府“回乡青年自主创业”的号召,某回乡青年带领全村多方筹集资金,流转耕地1000亩,全部用于种植李子和蔬菜,其中种植蔬菜的面积不少于种植李子的面积的4倍.(1)求该村种植蔬菜的面积至少为多少亩?
(2)今年村里按(1)中蔬菜种植面积的最小值种植蔬菜,李子和蔬菜上市后,李子每亩获利800元,蔬菜每亩获利600元,明年在保持李子种植面积不变的情况下,李子亩产量将上涨,预计每亩利润将增加3a%,同时利用新增流转耕地,使蔬菜种植面积扩大a%,并改善蔬菜种植结构,蔬菜每亩利润将增加a%,这样,明年李子和蔬菜的总利润将比今年的利润增加$\frac{12}{5}$a%,求a的值.
分析 (1)设该村种植蔬菜的面积为x亩,则该村种植李子的面积不多于$\frac{1}{4}$x亩,根据种植李子和蔬菜的总面积为1000亩即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其最小值即可得出结论;
(2)找出明年李子以及蔬菜的总利润,结合明年李子和蔬菜的总利润将比今年的利润增加$\frac{12}{5}$a%即可得出关于a的一元二次方程,解之取其正值即可.
解答 解:(1)设该村种植蔬菜的面积为x亩,则该村种植李子的面积不多于$\frac{1}{4}$x亩,
根据题意得:x+$\frac{1}{4}$x≥1000,
解得:x≥800.
答:种植蔬菜的面积至少为800亩.
(2)今年李子的种植面积为1000-800=200(亩),明年李子的总利润为200×800(1+3a%),
今年蔬菜种植面积为800(1+a%)亩,明年蔬菜的总利润为600(1+a%)×800(1+a%),
根据题意得:200×800(1+3a%)+600(1+a%)×800(1+a%)=(200×800+800×600)×(1+$\frac{12}{5}$a%),
整理得:a2-20a=0,
解得:a=20或a=0(舍去).
答:a的值为20.
点评 本题考查了一元一次不等式的应用以及一元二次方程的应用,解题的关键是:(1)根据种植的总面积列出关于x的一元一次不等式;(2)找准等量关系,列出关于a的一元一次方程.

练习册系列答案
相关题目
8.一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取1个球,则取到的是一个白球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
17. 如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米.
如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米.
 如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米.
如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为( )米.| A. | 4米 | B. | 5米 | C. | 7米 | D. | 8米 |
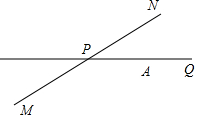 如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长?
如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长?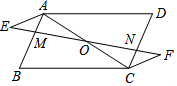 如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF. 如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]
如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.[注y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)]