题目内容
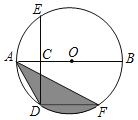
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,直径
,直径![]() 交弦
交弦![]() 于点
于点![]() .
.
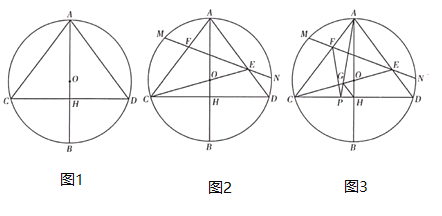
(1)如图1,求证:![]() ;
;
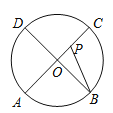
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,弦
,弦![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
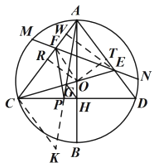
(3)如图3,在(2)的条件下,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接CO,DO,求出![]() ,根据三线合一证明
,根据三线合一证明![]() 即可;
即可;
(2)连接OF,过点O作OQ⊥MN于点Q,OR⊥AC于点R,OT⊥AD于点T,证明Rt△EOT≌Rt△FOR,可推出AE=CF;
(3)过点C作CK∥AD交AP的延长线于点K,过点E作EW⊥AF于点W,证△CPF≌△CPK,△CGK≌△EGA,求出DE=2GH=14,AC=25+14=39,CR=![]() ,再求出AW,CW的长,通过勾股定理求出EW,CE的长,推出CG的长,通过锐角三角函数求出OC的长,进一步可求出OG的长.
,再求出AW,CW的长,通过勾股定理求出EW,CE的长,推出CG的长,通过锐角三角函数求出OC的长,进一步可求出OG的长.
(1)证明:如图,连接![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ;
;
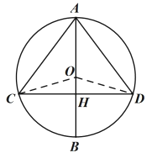
(2)证明:如图,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
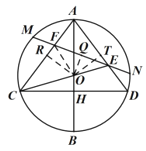
(3)解:如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在四边形![]() 中,
中,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 交
交![]() 的延长线点
的延长线点![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,∴
,∴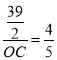 ,∴
,∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目