题目内容
【题目】.如图，圆柱底面半径为
，高为
，点
分别是圆柱两底面圆周上的点，且
、
在同一母线上，用一棉线从顺着圆柱侧面绕3圈到，求棉线最短为_________
。
【答案】
【解析】
将圆柱体展开，然后利用两点之间线段最短解答即可.
圆柱体的展开图如图所示：用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是：AC→CD→DB；即在圆柱体的展开图长方形中，将长方形平均分成3个小长方形，A沿着3个长方形的对角线运动到B的路线最短；
∵圆柱底面半径为2cm，
∴长方形的宽即是圆柱体的底面周长：2π×2=4πcm；
又∵圆柱高为9πcm，
∴小长方形的一条边长是3πcm；
根据勾股定理求得AC=CD=DB=5πcm；
∴AC+CD+DB=15πcm；
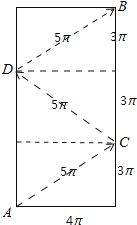
故答案为：15π．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
