题目内容
8.在△ABC中,AC=4,BC=3,AB=5,O是边AB的中点,以O为圆心,r为半径作⊙O.(1)当r满足0<r<$\frac{3}{2}$时,⊙O与△ABC的边有2个公共点;
(2)当r满足r=$\frac{3}{2}$或$\frac{5}{2}$时,⊙O与△ABC的边有3个公共点;
(3)当r满足$\frac{3}{2}$<r<2时,⊙O与△ABC的边有4个公共点.
分析 作OE⊥AC于点E,作OF⊥BC于点F,求得OE和OF,OC的长,结合图形即可解答.
解答  解:作OE⊥AC于点E,作OF⊥BC于点F.
解:作OE⊥AC于点E,作OF⊥BC于点F.
则OE=$\frac{1}{2}$BC=$\frac{3}{2}$,OF=$\frac{1}{2}$AC=2,OA=OC=OB=$\frac{5}{2}$.
(1)当0<r<$\frac{3}{2}$时,⊙O与△ABC的边有2个公共点,
故答案是:当0<r<$\frac{3}{2}$;
(2)当r=$\frac{3}{2}$或$\frac{5}{2}$时,⊙O与△ABC的边有3个公共点,
故答案是:r=$\frac{3}{2}$或$\frac{5}{2}$;
(3)当$\frac{3}{2}$<r<2时,⊙O与△ABC的边有4个公共点.
故答案是:$\frac{3}{2}$<r<2.
点评 本题考查了直线和圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
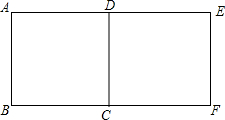 如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.
如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.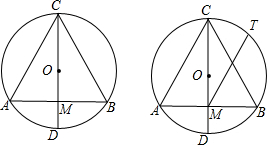
 如图所示,?ABCD中的对角线AC,BD相交于点O,线段EF经过点O,若?ABCD的周长为40cm,OE=4cm,则四边形ABFE的周长是28cm.
如图所示,?ABCD中的对角线AC,BD相交于点O,线段EF经过点O,若?ABCD的周长为40cm,OE=4cm,则四边形ABFE的周长是28cm.