题目内容
下列计算中,正确的是( )
| A、3x3•x4=3x12 |
| B、(x+y)2=x2+y2 |
| C、(a+2b)(a-2b)=a2-2b2 |
| D、m(m-1)=m2-m |
考点:平方差公式,单项式乘单项式,单项式乘多项式,完全平方公式
专题:计算题
分析:A、利用单项式乘以单项式法则计算得到结果,即可做出判断;
B、原式利用完全平方公式展开得到结果,即可做出判断;
C、原式利用平方差公式化简得到结果,即可做出判断;
D、原式利用单项式乘以多项式法则计算得到结果,即可做出判断.
B、原式利用完全平方公式展开得到结果,即可做出判断;
C、原式利用平方差公式化简得到结果,即可做出判断;
D、原式利用单项式乘以多项式法则计算得到结果,即可做出判断.
解答:解:A、3x3•x4=3x7,错误;
B、(x+y)2=x2+2xy+y2,错误;
C、(a+2b)(a-2b)=a2-4b2,错误;
D、m(m-1)=m2-m,正确,
故选D
B、(x+y)2=x2+2xy+y2,错误;
C、(a+2b)(a-2b)=a2-4b2,错误;
D、m(m-1)=m2-m,正确,
故选D
点评:此题考查了平方差公式,单项式乘单项式,单项式乘多项式,以及完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
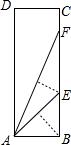 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则67.5°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则67.5°角的正切值是( )A、
| ||
B、
| ||
| C、2.5 | ||
D、
|
 如图所示,将一个边长为1的正方形分成四个全等的小正方形,再选右下角的小正方形进行第二次操作…重复这样的操作,则经过2014次操作后右下角的小正方形面积是( )
如图所示,将一个边长为1的正方形分成四个全等的小正方形,再选右下角的小正方形进行第二次操作…重复这样的操作,则经过2014次操作后右下角的小正方形面积是( )A、
| ||
B、(
| ||
C、(
| ||
D、1-(
|
下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A、 |
B、 |
C、 |
D、 |
已知α是锐角,且sinα=0.75,则( )
| A、0°<α<30° |
| B、30°<α<45° |
| C、45°<α<60° |
| D、60°<α<90° |
