题目内容
19.验证:$2\sqrt{\frac{2}{3}}$=$\sqrt{2+\frac{2}{3}}$.验证:2$\sqrt{\frac{2}{3}}$=$\sqrt{{2}^{2}}$×$\sqrt{\frac{2}{3}}$=$\sqrt{\frac{{2}^{2}×2}{3}}$=$\sqrt{\frac{{2}^{3}}{3}}$=$\sqrt{\frac{({2}^{3}-2)+2}{3}}$=$\sqrt{\frac{{2}^{3}-2}{{2}^{2}-1}+\frac{2}{{2}^{2}-1}}$=$\sqrt{\frac{2({2}^{2}-1)}{{2}^{2}-1}+\frac{2}{{2}^{2}-1}}$=$\sqrt{2+\frac{2}{3}}$.
请你模仿上面等式的验证方法验证:3$\sqrt{\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$.
验证:
同理可得:4$\sqrt{\frac{4}{15}}$=$\sqrt{4+\frac{4}{15}}$,…
请用含有自然数n(n>1)的等式表示上述等式的规律.
分析 根据已知结合二次根式的性质化简求出,进而得出数字之间规律进而得出得出答案即可.
解答 解:3$\sqrt{\frac{3}{8}}$=$\sqrt{{3}^{2}×\frac{3}{8}}$=$\sqrt{\frac{{3}^{3}}{8}}$=$\sqrt{\frac{({3}^{3}-3)+3}{8}}$=$\sqrt{\frac{{3}^{3}-3}{{3}^{2}-1}+\frac{3}{{3}^{2}-1}}$=$\sqrt{\frac{3({3}^{2}-1)}{{3}^{2}-1}+\frac{3}{{3}^{2}-1}}$=$\sqrt{3+\frac{3}{8}}$,
4$\sqrt{\frac{4}{15}}$=$\sqrt{4+\frac{4}{15}}$;
含有自然数n(n>1)的等式表示上述等式的规律:n$\sqrt{\frac{n}{{n}^{2}-1}}$=$\sqrt{n+\frac{n}{{n}^{2}-1}}$.
故答案为:$\sqrt{4+\frac{4}{15}}$.
点评 此题主要考查了二次根式的性质与化简,正确得出数字变化规律是解题关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
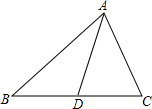 如图,AD是△ABC的中线,若AB=8cm,AC=6cm,则△ABD和△ACD的周长之差为2cm.
如图,AD是△ABC的中线,若AB=8cm,AC=6cm,则△ABD和△ACD的周长之差为2cm.