��Ŀ����
19����ͼ�٣����㹻��ı߳�Ϊa��С�����Σ�A�ࣩ����Ϊa��Ϊb�ij����Σ�B�ࣩ�Լ��߳�Ϊb�Ĵ������Σ�C�ࣩ����������ͼ���е����ֲ��ϸ����ɿ���ƴ��һЩ������������ijЩ��ʽ�� ����ͼ�ڿ��Խ���Ϊ����a+2b����a+b��=a2+3ab+2b2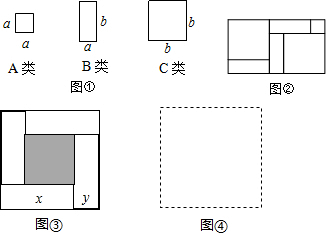
��1��ȡͼ���е����ɸ�������ͼ�ζ�Ҫȡ����ƴ��һ�������Σ�ʹ�����Ϊ��2a+b����a+2b��������ͼ������л���ͼ�Σ�������ͼ�λش�2a+b����a+2b��=2a2+5ab+2b2��
��2����ȡ���е����ɸ�������ͼ�ζ�Ҫȡ����ƴ��һ�������Σ�ʹ�����Ϊa2+5ab+6b2��
���㻭��ͼ����C�Ƭ6�ţ�
�ڿɽ�����ʽa2+5ab+6b2�ֽ���ʽΪ��a+2b����a+3b��
��3����ͼ�ۣ��������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ����ε����߳���x��y�����۲�ͼ�����жϣ�����ȷ��ϵʽ�������д�ں����Ϣ٢ڢۢܣ���д��ţ�
��xy=$\frac{{m}^{2}-{n}^{2}}{4}$ ��x+y=m ��x2-y2=m•n ��x2+y2=$\frac{{m}^{2}+{n}^{2}}{2}$��
���� ��1���������⻭��ͼ�Σ���ͼ��ʾ�����ɵõ������
��2�����ݵ�ʽ���ɵó���6�ţ�����ͼ�κ������ʽ�ó����ɣ�
��3����������ó�x+y=m��m2-n2=4xy������ƽ���ʽ����ȫƽ����ʽ�жϼ��ɣ�
��� �⣺��1����2a+b����a+2b��=2a2+5ab+2b2��
�ʴ�Ϊ��2a2+5ab+2b2��
��2���١߳����ε����Ϊa2+5ab+6b2��
���ͼ����ҪC�Ƭ6�ţ�
�ʴ�Ϊ��6��
��a2+5ab+6b2=��a+2b����a+3b����
�ʴ�Ϊ����a+2b����a+3b����
��3���⣺����ͼ�۵ã�x+y=m��
��m2-n2=4xy��
��xy=$\frac{{m}^{2}-{n}^{2}}{4}$��
x2-y2=��x+y����x-y��=mn��
��x2+y2=��x+y��2-2xy=m2-2��$\frac{{m}^{2}-{n}^{2}}{4}$=$\frac{{m}^{2}+{n}^{2}}{2}$��
��ѡ��٢ڢۢܶ���ȷ��
�ʴ�Ϊ���٢ڢۢܣ�
���� ���⿼���˷ֽ���ʽ�������ε������ƽ���ʽ����ȫƽ����ʽ��Ӧ�ã���Ҫ����ѧ���Ĺ۲�ͼ�ε������ͻ���������

��ϰ��ϵ�д�
�����Ŀ
10������x2-x+m����x-8���в���x��һ�����m��ֵΪ��������
| A�� | 8 | B�� | -8 | C�� | 0 | D�� | 8��-8 |
4�������ж���ʽ�˷������У���������ƽ���ʽ����������ǣ�������
| A�� | ��2x+3y�� ��-2x+3y�� | B�� | ��a-2b�� ��a+2b�� | C�� | ��-x-2y�� ��x+2y�� | D�� | ��-2x-3y�� ��3y-2x�� |
8����5-2����-5��2��-��-5��2��-|-5|����-5��-2��-5-2�У������ĸ���Ϊ��������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
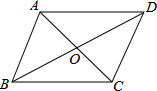 ��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O��������һ������AB=AD��ʹ?ABCD��Ϊ���Σ�д�����������һ���������ɣ�
��ͼ����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O��������һ������AB=AD��ʹ?ABCD��Ϊ���Σ�д�����������һ���������ɣ�