题目内容
17. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以AB为直径作半圆O交BC于点D,过点D的切线交AC于点E,BE交⊙O于点F,AF的延长线与DE相交于点P.若OA=l,则EB=$\sqrt{7}$,PE=$\frac{12-2\sqrt{3}}{11}$.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以AB为直径作半圆O交BC于点D,过点D的切线交AC于点E,BE交⊙O于点F,AF的延长线与DE相交于点P.若OA=l,则EB=$\sqrt{7}$,PE=$\frac{12-2\sqrt{3}}{11}$.
分析 (1)根据条件求出AC,证明AE=EC,在RT△AEB中可以解决问题.
(2)如图过点D作MN⊥AB,交AP的延长线于N,由DN∥AE得$\frac{PE}{PD}$=$\frac{AE}{DN}$,求出DN就可以了.
解答  解:①连接OD,
解:①连接OD,
∵∠C=30°,∠BAC=90°,
∴∠ABC=60°,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴∠AOD=120°,
∵BA⊥AC,
∴AE是⊙O的切线,
∵ED是⊙O的切线,
∴AE=DE,∠AED=60°,
∵∠AED=∠C+∠CDE,
∴∠CDE=30°,
∴CE=DE,
∵OA=1,
∴AB=2,
∴AC=2$\sqrt{3}$,
∴AE=EC=$\sqrt{3}$,
∴BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\sqrt{7}$.
②如图过点D作MN⊥AB,交AP的延长线于N,连接AD. 在RT△ABC中,∵∠C=30°,AB=2
在RT△ABC中,∵∠C=30°,AB=2
∴BC=4,AC=2$\sqrt{3}$,
∵$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AB•AC,
∴AD=$\sqrt{3}$,
∵AB是直径,
∴∠ADB=∠ADC=90°,∠AFB=∠AFE=90°,
∴∠CAD=60°,∠DAM=30°,
∴DM=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,AM=$\frac{3\sqrt{3}}{2}$,
∵∠FAB+∠ABE=90°,∠AEB+∠B=90°,
∴∠AEB=∠MAN,
∵∠AMN=∠EAB,
∴△AMN∽△EAB,
∴$\frac{MN}{AB}=\frac{AM}{AE}$,
∴$\frac{MN}{2}=\frac{\frac{3\sqrt{3}}{2}}{\sqrt{3}}$,
∴MN=3,DN=MN-DM=3-$\frac{\sqrt{3}}{2}$,
∵DN∥AE,
∴$\frac{DN}{AE}$=$\frac{PD}{PE}$,
∴$\frac{3-\frac{\sqrt{3}}{2}}{\sqrt{3}}=\frac{\sqrt{3}-PE}{PE}$,
∴PE=$\frac{12-2\sqrt{3}}{11}$.
点评 本题考查了切线长定理、切线的性质、勾股定理、平行成比例等知识,利用平行成比例添加辅助线是解决问题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案 已知双曲线y=$\frac{k}{x}$上有两点A(-1,-2),B(1,a),直线y=-x+a,P是双曲线第一象限上一动点.
已知双曲线y=$\frac{k}{x}$上有两点A(-1,-2),B(1,a),直线y=-x+a,P是双曲线第一象限上一动点.
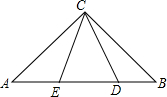 如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )
如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )