题目内容
13.如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
分析 (1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,求出∠ABF=135°,∠ABF=∠ACD,证出BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;
(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;
(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
解答 (1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABF=∠ACD}\\{BF=CD}\end{array}\right.$,
∴△ABF≌△ACD(SAS),
∴AD=AF;
(2)证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中,
$\left\{\begin{array}{l}{AE=AB}&{\;}\\{∠EAF=∠BAD}&{\;}\\{AF=AD}&{\;}\end{array}\right.$,
∴△AEF≌△ABD(SAS),
∴BD=EF;
(3)解:四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
由(2)知,∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、正方形的判定、矩形的判定;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

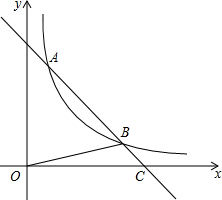 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个,或1个,或2个 |
| A. | x≥-2 | B. | x≥-2且x≠0 | C. | x≠0 | D. | x>0且x≠-2 |
| A. | (-2a3)2=-4a6 | B. | $\sqrt{9}$=±3 | C. | m2•m3=m6 | D. | x3+2x3=3x3 |
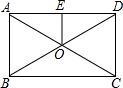 如图,已知:矩形ABCD中对角线,AC,BD交于点O,E是AD中点,连接OE.若OE=3,AD=8,则对角线AC的长为( )
如图,已知:矩形ABCD中对角线,AC,BD交于点O,E是AD中点,连接OE.若OE=3,AD=8,则对角线AC的长为( )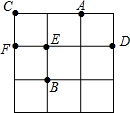 如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$.
如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$. 如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为17°.
如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为17°.