题目内容
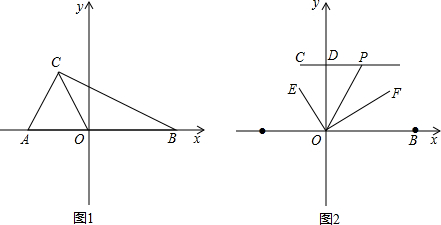
12.在平面直角坐标系中,A(a,0),B(b,0),C(-1,2)(见图1),且|a+2|+(b-3)2=0(1)求a、b的值;
(2)①在x轴的正半轴上存在一点M,使△COM的面积=$\frac{1}{2}$△ABC的面积,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积=$\frac{1}{2}$△ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,$\frac{∠OPD}{∠DOE}$的值是否会改变?若不变,求其值;若改变,说明理由
分析 (1)根据非负数的性质得a+2=0,b-3=0,然后解一次方程即可得到a与b的值;
(2)①设M(t,0),根据三角形面积公式可计算出S△ABC=5,由于△COM的面积=$\frac{1}{2}$△ABC的面积,则$\frac{1}{2}$•t•2=$\frac{1}{2}$×5,然后解方程求出t即可得到M点坐标;
②分类讨论:当M点在x轴的负半轴上时,易得M点坐标为(-$\frac{5}{2}$,0);当M点在y轴的轴上时,设M点坐标为(0,m),根据三角形面积公式得到$\frac{1}{2}$•|m|•1=$\frac{1}{2}$×5,然后解方程求出t即可得到M点坐标;
(3)如图2,由OE平分∠AOP得到∠AOE=∠POE=∠1+∠2,根据垂直的定义得到∠1+∠2+∠3=90°,∠4+∠AOE=90°,于是得到∠3=∠4,接着证明CD∥AB,利用平行线的性质得∠OPD=∠POB=2∠3,
然后利用∠1+∠2+∠3=90°,∠2+∠3+∠4=90°可得∠1=∠3,则可计算出$\frac{∠OPD}{∠DOE}$=2.
解答 解:(1)∵|a+2|+(b-3)2=0
∴a+2=0,b-3=0,
∴a=-2,b=3;
(2)①设M(t,0),
S△ABC=$\frac{1}{2}$×(3+2)×2=5,
∵△COM的面积=$\frac{1}{2}$△ABC的面积,
∴$\frac{1}{2}$•t•2=$\frac{1}{2}$×5,解得t=$\frac{5}{2}$,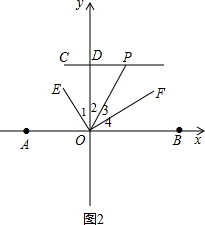
∴M点坐标为($\frac{5}{2}$,0);
②当M点在x轴的负半轴上时,M点坐标为(-$\frac{5}{2}$,0);
当M点在y轴的轴上时,设M点坐标为(0,m),则$\frac{1}{2}$•|m|•1=$\frac{1}{2}$×5,解得m=±5,此时M点坐标为(0,5)或(0,-5);
(3)$\frac{∠OPD}{∠DOE}$的值不会改变.
如图2,
∵OE平分∠AOP,
∴∠AOE=∠POE=∠1+∠2,
∵OF⊥OE,
∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,
∴∠3=∠4,
∵CD⊥y轴,
∴CD∥AB,
∴∠OPD=∠POB=2∠3,
∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,
∴∠1+∠2+∠3=∠2+2∠3,
∴∠1=∠3,
∴$\frac{∠OPD}{∠DOE}$=$\frac{2∠3}{∠1}$=2.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住特殊位置点的坐标特征.也考查了三角形面积公式和平行线的性质.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | 阴天一定会下雨 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 在五个抽屉中任意放入6本书,则至少有一个抽屉里有两本书 |

| A. | 5π | B. | $\frac{3π}{2}$ | C. | $\frac{13π}{2}$ | D. | $\frac{23π}{2}$ |
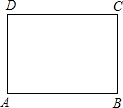 如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)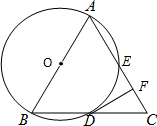 如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.
如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.