题目内容
17.菱形的边长是6,且有一个内角为60°,则菱形的面积是( )| A. | 36$\sqrt{3}$ | B. | 18$\sqrt{3}$ | C. | 36 | D. | 9$\sqrt{3}$ |
分析 首先根据题意画出图形,然后过点D作DE⊥AB于点E,由菱形的边长是6,可求得AB=AD=6,又由有一个内角为60°,可求得其高,继而求得答案.
解答 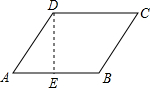 解:如图,过点D作DE⊥AB于点E,∠A=60°,
解:如图,过点D作DE⊥AB于点E,∠A=60°,
∵菱形的边长是6,
∴AB=AD=6,
∵在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=3,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=3$\sqrt{3}$,
∴该菱形的面积=AB•DE=18$\sqrt{3}$.
故选(B).
点评 此题主要考查了菱形的性质、含30°角的直角三角形的性质以及勾股定理的综合应用.注意菱形的四条边都相等,菱形的面积等于底乘高.

练习册系列答案
相关题目
8.如果不等式组$\left\{\begin{array}{l}2x-1>3(x-1)\\ x>m\end{array}$无解,那么m的取值范围是( )
| A. | m=2 | B. | m>2 | C. | m<2 | D. | m≥2 |
5.顺次连接对角线垂直的?ABCD各边中点所得四边形必定是( )
| A. | 平行四边形 | B. | 菱形 | C. | 正方形 | D. | 矩形 |
12.已知a<0<b,那么下列不等式组中一定有解的是( )
| A. | $\left\{\begin{array}{l}x>-a\\ x<-b\end{array}\right.$ | B. | $\left\{\begin{array}{l}x>-b\\ x<-a\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>a\\ x<-b\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-a\\ x<b\end{array}\right.$ |
9.点M(a,5)与点N(2,b)关于x轴对称,则a、b的值分别是( )
| A. | -2,-5 | B. | 2,5 | C. | -2,5 | D. | 2,-5 |
6.若|a|=8,则$\frac{a+8}{2}$的值为( )
| A. | 0 | B. | 0或8 | C. | 4 | D. | -8或8 |