题目内容
3.列方程或方程组解应用题:为打造刺猬河沿岸的风光带,有一段长为360米的河道整治任务由A、B两个工程队先后接力完成.A工程队每天整治24米,B工程队每天整治16米,共用时20天.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲:$\left\{\begin{array}{l}x+y=\\ \\ 24x+16y=\end{array}\right.$乙:$\left\{\begin{array}{l}x+y=\\ \frac{x}{24}+\frac{y}{16}=\end{array}\right.$
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,并且在方框中补全甲、乙两名同学所列的方程组:
甲:x表示A队的工作时间,y表示B队的工作时间;
乙:x表示A队的工作量,y表示B队的工作量.
(2)求出其中一个方程组的解,并回答A、B两工程队分别整治河道多少米?
分析 (1)根据甲、乙两名同学所列的方程组可得,甲:x表示A队的工作时间,y表示B队的工作时间;乙:x表示A队的工作量,y表示B队的工作量,补全方程组即可;
(2)根据二元一次方程组的解法求解方程组甲.
解答 解:(1)甲:$\left\{\begin{array}{l}{x+y=20}\\{24x+16y=360}\end{array}\right.$;
乙:$\left\{\begin{array}{l}{x+y=360}\\{\frac{x}{24}+\frac{y}{36}=20}\end{array}\right.$;
甲:x表示A队的工作时间,y表示B队的工作时间;乙:x表示A队的工作量,y表示B队的工作量;
(2)由方程组甲得:$\left\{\begin{array}{l}x=5\\ y=15\end{array}\right.$,
则24x=120,16y=240,
答:A队整治河道120米,B队整治河道240米.
故答案为:A队的工作时间,B队的工作时间;A队的工作量,B队的工作量.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,正确找出题目中的相等关系,列方程组求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若关于x的方程x2-3x+a=0的一个根是1,则a的值为( )
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
14.下列语句中,正确的是( )
| A. | 一个实数的平方根有两个,它们互为相反数 | |
| B. | 负数没有立方根 | |
| C. | 立方根是这个数本身的数只有两个 | |
| D. | 实数与数轴上的点是一一对应的 |
11.已知关于x的一元二次方程(x-1)2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个实数根 |
18.计算$\frac{1}{a-1}-\frac{a}{a-1}$的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1+a}{a-1}$ | D. | 2 |
 如图,△ABC中,∠ACB=80°,D为BC延长线上一点,且∠BAC=∠D,求∠BAD的度数.
如图,△ABC中,∠ACB=80°,D为BC延长线上一点,且∠BAC=∠D,求∠BAD的度数.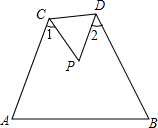 如图,△ABP沿CD折叠,求证:∠1+∠2=2∠P.
如图,△ABP沿CD折叠,求证:∠1+∠2=2∠P.