题目内容
在(ax2+bx-3)(x2-
x+8)的结果中不含x3和x项,则a= ,b= .
| 1 |
| 2 |
考点:多项式乘多项式
专题:
分析:首先利用多项式乘法法则计算出(ax2+bx-3)(x2-
x+8),再根据积不含x3和x项,可得含x3的项和含x的项的系数等于零,即可求出a与b的值.
| 1 |
| 2 |
解答:解:(ax2+bx-3)(x2-
x+8)
=ax4-
ax3+8ax2+bx3-
bx2+8bx-3x2+
x-24
=ax4+(-
a+b)x3+(8a-
b-3)x2+(8b+
)x-24,
∵积不含x3的项,也不含x的项,
∴-
a+b=0,8b+
=0,
解得:b=-
,a=-
,
故答案为:-
,-
.
| 1 |
| 2 |
=ax4-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=ax4+(-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵积不含x3的项,也不含x的项,
∴-
| 1 |
| 2 |
| 3 |
| 2 |
解得:b=-
| 3 |
| 16 |
| 3 |
| 8 |
故答案为:-
| 3 |
| 8 |
| 3 |
| 16 |
点评:此题主要考查了多项式乘以多项式,关键是掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
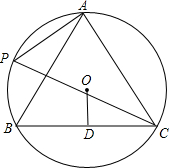 如图,A、P、B、C是半径为8的⊙O上的四点,且△ABC为等边三角形.
如图,A、P、B、C是半径为8的⊙O上的四点,且△ABC为等边三角形. 如图,圆柱的底面半径为2cm,点B距离底面8cm,从底面上的点绕曲面到达点B的最近距离
如图,圆柱的底面半径为2cm,点B距离底面8cm,从底面上的点绕曲面到达点B的最近距离 如图,已知线段AB、CD相交于点O,且∠A=∠B,只需补充一个条件
如图,已知线段AB、CD相交于点O,且∠A=∠B,只需补充一个条件