题目内容
10.有一列式子,按一定规律排列成-5a2,25a5,-125a10,625a17,-3125a26,….(1)当a=1时,其中三个相邻数的和是525,则位于这三个数中间的数是-125;
(2)上列式子中第n个式子为(-5)n${a}^{{n}^{2}+1}$(n为正整数,用n和a的式子表示).
分析 (1)a=1时,可知该数列式-5,25,-125,625,…找出其中的规律即可求出答案.
(2)题意可知,该列单项式的系数按照(-5)n进行变化,次数按照n2+1进行变化,
解答 解:(1)(1)a=1时,可知该数列式-5,25,-125,625,…,
∴第n个数可以表示为:(-5)n,
∴设相邻的三个数为:(-5)n-1、(-5)n、(-5)n+1,
∴(-5)n-1+(-5)n+(-5)n+1=525=52×21
∴(-5)n[(-5)-1+1-5]=52×21
∴(-5)n×$\frac{-21}{5}$=52×21
∴(-5)n=-53
∴(-5)n=(-5)3
∴n=3,
∴中间的数为(-5)3=-125
(2)该列单项式的系数按照(-5)n进行变化,次数按照n2+1进行变化,
∴第n个式子为:(-5)n${a}^{{n}^{2}+1}$
故答案为:(1)-125;(2)(-5)n${a}^{{n}^{2}+1}$
点评 本题考查单项式的概念,涉及数字规律问题,属于基础中等题型.

练习册系列答案
相关题目
20.商场将标价为300元/件的某种服装打八折销售,每件仍可获利80元,则这种服装每件的标价比进价多( )
| A. | 100元 | B. | 120元 | C. | 140元 | D. | 160元 |
1.设点A(-3,a),B(b,$\frac{1}{2}$)在同一个正比例函数的图象上,则ab的值为( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -6 | D. | $\frac{3}{2}$ |
18.在直线l上截取线段AB,使AB=6cm,再截取BC,使BC=3cm,则线段AC的长为( )
| A. | 9cm | B. | 3cm | C. | 3cm或9cm | D. | 6cm或9cm |
5.在平面直角坐标系中,将抛物线y=x2+2x+3绕着原点旋转180°,所得抛物线的解析式是( )
| A. | y=(x+1)2-2 | B. | y=-(x-1)2-2 | C. | y=-(x-1)2+2 | D. | y=(x-1)2-2 |
 如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.
如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.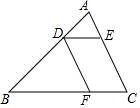 如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.
如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.