题目内容
5．用配方法说明：无论x取何值，代数式x2-4x+5的值总大于0，再求出当x取何值时，代数式x2-4x+5的值最小？最小值是多少？分析 首先将原式变形为（x-2）2+1，根据非负数的意义就可以得出代数式的值总是正数，并且当（x-2）2=0，即x=2时，代数式x2-4x+5有最小值．
解答 解：x2-4x+5
=x2-4x+4+1
=（x-2）2+1
∵（x-2）2≥0，
∴（x-2）2+1＞0，
∴代数式x2-8x+17的值都大于零；
当（x-2）2=0，即x=2时，代数式x2-4x+5有最小值，最小值为1．
点评 本题考查了配方法的应用：配方法的理论依据是公式a2±2ab+b2=（a±b）2．二次三项式是完全平方式，则常数项是一次项系数一半的平方．
练习册系列答案
相关题目
13．用配方法解方程x2+2x=8的解为（ ）
| A． | x1=4，x2=-2 | B． | x1=-10，x2=8 | C． | x1=10，x2=-8 | D． | x1=-4，x2=2 |
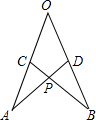如图所示，在∠AOB的两边截取AO=BO，CO=DO，连结AD、BC交于点P，考察下列结论，其中正确的是（ ）