题目内容
解方程
(1)(x-2)2+x(x-2)=0
(2)x2+2x+1=(3+2x)2.
(1)(x-2)2+x(x-2)=0
(2)x2+2x+1=(3+2x)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程利用因式分解法求出解即可;
(2)方程变形后,利用平方根定义开方即可求出解.
(2)方程变形后,利用平方根定义开方即可求出解.
解答:解:(1)分解因式得:(x-2)(x-2+x)=0,
可得x-2=0或2x-2=0,
解得:x1=2,x2=1;
(2)x2+2x+1=(3+2x)2
变形得:(x+1)2=(3+2x)2,
开方得:x+1=±3+2x,
解得:x1=-2,x2=-
.
可得x-2=0或2x-2=0,
解得:x1=2,x2=1;
(2)x2+2x+1=(3+2x)2
变形得:(x+1)2=(3+2x)2,
开方得:x+1=±3+2x,
解得:x1=-2,x2=-
| 4 |
| 3 |
点评:此题考查了解一元二次方程-因式分解法与直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
在△ABC中,AB=4cm,BC=7cm,则AC的长可能是( )
| A、2cm | B、3cm |
| C、5cm | D、12cm |
下列各组长度的线段能构成三角形的是( )
| A、3cm,4cm,8cm |
| B、5cm,6cm,11cm |
| C、6cm,1cm,6cm |
| D、4cm,10cm,4m |
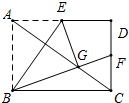 在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.
在矩形ABCD中,点E是边AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形的对角线AC上,连接BG并延长交CD于F.求证:点F是CD的中点.