题目内容
13. 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为$\frac{4}{5}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为$\frac{4}{5}$.
分析 首先利用勾股定理计算出BC长,然后再利用直角三角形的面积公式计算出CD长,再用余弦定义可得答案.
解答 解:∵AC=4,AB=5,∠ACB=90°,
∴BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴$\frac{5}{2}$CD=6,
CD=$\frac{12}{5}$,
∴cos∠BCD=$\frac{DC}{BC}$=$\frac{\frac{12}{5}}{3}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 此题主要考查了锐角三角函数的定义,以及勾股定理的应用,关键是掌握余弦=$\frac{邻边}{斜边}$.

练习册系列答案
相关题目

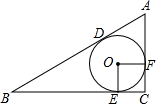 如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°,
如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°,