Question

20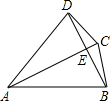．如图，AC平分∠DAB，AD=AC=AB，如下四个结论：①AC⊥BD；②BC=DE；③∠DBC=$\frac{1}{2}$∠DAC；④△ABC是正三角形，正确的结论有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 由等腰三角形的性质得出①正确；由线段垂直平分线的性质得出②错误；由圆周角定理得出③正确；由正三角形的性质得出④错误，即可得出结论．

解答 解：∵AB=AC，AC=AD，
∴AB=AD
∵AC平分∠DAB
∴AC⊥BD，BE=DE，①正确；
∴DC=CB，
∵DC＞DE，
∴BC＞DE，②错误；
D、C、B可看作是以点A为圆心的圆上，
根据圆周角定理，得∠DBC=$\frac{1}{2}$∠DAC，③正确；
当△ABC是正三角形时，∠CAB=60°
那么∠DAB=120°，
故④是不一定成立的，所以错误．
正确的有2个．
故选：B．

点评 本题考查了等腰三角形的性质及垂直平分线的性质；利用等腰三角形的三线合一是常用的判断方法；注意把图形放入圆中解决可使问题简化．