题目内容
12. 如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )
如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )| A. | 4$\sqrt{2}$ | B. | 5$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
分析 根据勾股定理:直角三角形斜边的平方等于两直角边的平方和,可得答案.
解答 解:由勾股定理,得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
AD=$\sqrt{A{C}^{2}+A{D}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,
AG=$\sqrt{A{F}^{2}+F{G}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$4$\sqrt{2}$,
故选:A.
点评 本题考查了勾股定理,利用勾股定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列运算正确的是( )
| A. | x4+x4=2x8 | B. | x3•x=x4 | C. | (x-y)2=x2-y2 | D. | (x2)3=x5 |
4.把抛物线y=-x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x+3)2+1 | B. | y=-(x+1)2+3 | C. | y=-(x-1)2+4 | D. | y=-(x+1)2+4 |
2.经统计2012年某市中考考生人数达56940人,数据56940用科学记数法可以表示为(要求保留三位有效数字)( )
| A. | 56.950×103 | B. | 5.6950×104 | C. | 5.70×104 | D. | 5.69×104 |
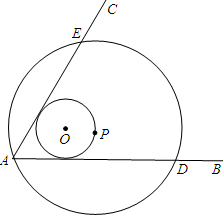 如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.
如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.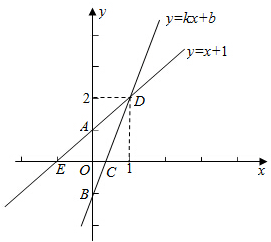 如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.
如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.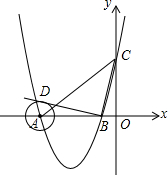 如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).