Question

7．如图，已知△ABC是等边三角形，且CE=AD．求证：DF=EF．

Answer 1

分析 作DG∥BC交AC于G，先证明△ADG是等边三角形，得出AD=GD，于是得到DG=CE，然后证得△DFG≌△EFC，根据全等三角形的性质即可得出结论．

解答 证明：作DG∥BC交AC于G，如图所示：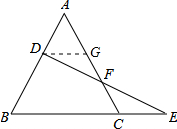
则∠DGF=∠ECF，
∵△ABC是等边三角形，
∴∠A=∠B=∠ACB=60°，
∵DG∥BC，
∴∠ADG=∠B，∠AGD=∠ACB，
∴∠A=∠ADG=∠AGD，
∴△ADG是等边三角形，
∴AD=GD，
∵AD=CE，
∴DG=CE，
在△DFG和△EFC中，$\left\{\begin{array}{l}{∠DGF=∠ECF}\\{∠DFG=∠EFC}\\{DG=CE}\\{\;}\end{array}\right.$，
∴△DFG≌△EFC（AAS），
∴DF=EF．

点评 本题考查了全等三角形的判定与性质、等边三角形的判定与性质；熟练掌握等边三角形的判定与性质，并能进行推理论证是解决问题的关键．