题目内容
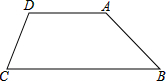 如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为
如图所示,拦水坝横截面为等腰梯形ABCD,背水坡AB坡度为| 3 |
(1)求拦水坝的高度及背水坡的长;
(2)求拦水坝的横截面积.
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)利用坡比的概念以及勾股定理得出AB以及AE的长;
(2)利用(1)中所求,再结合梯形面积公式求出即可.
(2)利用(1)中所求,再结合梯形面积公式求出即可.
解答: 解:(1)如图所示:过点A作AE⊥BC于点E,
解:(1)如图所示:过点A作AE⊥BC于点E,
∵拦水坝横截面为等腰梯形ABCD,梯形上底10米,下底为30米,
∴BE=10m,
∵背水坡AB坡度为
:1,
∴AE=10
m,
∴AB=20m,
即拦水坝的高度为10
m,背水坡的长为20m;
(2)拦水坝的横截面积为:
(AD+BC)×AE=
(10+30)×10
=200
(m2).
 解:(1)如图所示:过点A作AE⊥BC于点E,
解:(1)如图所示:过点A作AE⊥BC于点E,∵拦水坝横截面为等腰梯形ABCD,梯形上底10米,下底为30米,
∴BE=10m,
∵背水坡AB坡度为
| 3 |
∴AE=10
| 3 |
∴AB=20m,
即拦水坝的高度为10
| 3 |
(2)拦水坝的横截面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查了解直角三角形的应用以及梯形面积求法,熟练掌握坡比的定义是解题关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
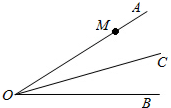 如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是
如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是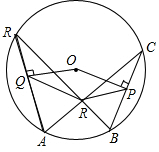 如图,已知AC、BD是⊙O的两条相互垂直的弦,并且AC、BD相交于点R,OP⊥BC,OQ⊥AD.求证:四边形OPRQ为平行四边形.
如图,已知AC、BD是⊙O的两条相互垂直的弦,并且AC、BD相交于点R,OP⊥BC,OQ⊥AD.求证:四边形OPRQ为平行四边形.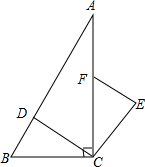 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后的CE,连接EF.当CD⊥AB时,判断EF与CD的位置关系,并说明理由.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后的CE,连接EF.当CD⊥AB时,判断EF与CD的位置关系,并说明理由.