题目内容
9.在平面直角坐标系中,若一个点的横纵坐标互为相反数,则该点一定不在( )| A. | 直线y=-x上 | B. | 直线y=x上 | C. | 双曲线y=$\frac{1}{x}$ | D. | 抛物线y=x2上 |
分析 分别根据一次函数、反比例函数及二次函数图象上点的坐标特点进行分析即可.
解答 解:A、若此点坐标是(0,0)时,在直线y=-x上,故本选项错误;
B、若此点坐标是(0,0)时,在直线y=x上,故本选项错误;
C、因为双曲线y=$\frac{1}{x}$上的点必须符合xy=1,故x、y同号与已知矛盾,故本选项正确;
D、若此点坐标是(0,0)时,在抛物线y=x2上,故本选项错误.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
20.已知关于x的方程m2x2+(4m-1)x+4=0的两个实数根互为倒数,那么m的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
19. 如图,假设可以在图中每个小正方形内任意取点(每个小正方形除颜色外完全相同),那么这个点取在阴影部分的概率是( )
如图,假设可以在图中每个小正方形内任意取点(每个小正方形除颜色外完全相同),那么这个点取在阴影部分的概率是( )
 如图,假设可以在图中每个小正方形内任意取点(每个小正方形除颜色外完全相同),那么这个点取在阴影部分的概率是( )
如图,假设可以在图中每个小正方形内任意取点(每个小正方形除颜色外完全相同),那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{6}{25}$ | C. | $\frac{7}{25}$ | D. | $\frac{8}{25}$ |
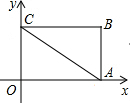 如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.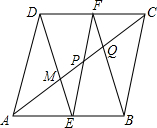 如图,菱形ABCD的边长为4,E、F分别是AB、CD中点,连接DE、EF、FB分别交AC于M、P、Q,且DE=4,求PQ的长.
如图,菱形ABCD的边长为4,E、F分别是AB、CD中点,连接DE、EF、FB分别交AC于M、P、Q,且DE=4,求PQ的长.