题目内容
20.已知关于x的方程m2x2+(4m-1)x+4=0的两个实数根互为倒数,那么m的值为( )| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
分析 先根据根与系数的关系得到$\frac{4}{{m}^{2}}$=1,解得m=2或m=-2,然后根据判别式的意义确定满足条件的m的值.
解答 解:∵方程m2x2+(4m-1)x+4=0的两个实数根互为倒数,
∴$\frac{4}{{m}^{2}}$=1,解得m=2或m=-2,
当m=2时,方程变形为4x2+7x+4=0,△=49-4×4×4<0,方程没有实数解,
所以m的值为-2.
故选B.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.下列式子运算正确的是( )
| A. | (2a+b)(2a-b)=2a2-b2 | B. | (a+2)(b-1)=ab-2 | C. | (a+1)2=a2+1 | D. | (x-1)(x-2)=x2-3x+2 |
9.在平面直角坐标系中,若一个点的横纵坐标互为相反数,则该点一定不在( )
| A. | 直线y=-x上 | B. | 直线y=x上 | C. | 双曲线y=$\frac{1}{x}$ | D. | 抛物线y=x2上 |
10.在平面直角坐标系中,点A(1,2)的横坐标为( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
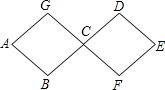 如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014米停下,则这个微型机器人所停的点是( )
如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2014米停下,则这个微型机器人所停的点是( )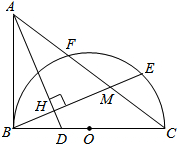 如图,已知△ABC,以BC为直径,O为圆心的半圆交AC于点E,点E为弧CF的中点,连接BE交AC于点M,AD为△ABC的角平分线交BC于点D,且AD⊥BE,垂足为点H
如图,已知△ABC,以BC为直径,O为圆心的半圆交AC于点E,点E为弧CF的中点,连接BE交AC于点M,AD为△ABC的角平分线交BC于点D,且AD⊥BE,垂足为点H