题目内容
14.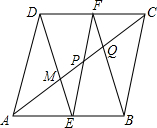 如图,菱形ABCD的边长为4,E、F分别是AB、CD中点,连接DE、EF、FB分别交AC于M、P、Q,且DE=4,求PQ的长.
如图,菱形ABCD的边长为4,E、F分别是AB、CD中点,连接DE、EF、FB分别交AC于M、P、Q,且DE=4,求PQ的长.
分析 作DH⊥AB于H,CQ⊥AB于Q,如图,根据菱形的性质得AD=AB=CD=4,CD∥AB,则DF=BE=2,于是可判断四边形DEBF为平行四边形,得到PM=PQ,DE∥BF,则ME为△ABQ的中位线,所以AM=MQ,同理可得CQ=MQ,于是得到PQ=$\frac{1}{6}$AC;由于AD=DE=4,DH⊥AE,根据等腰三角形的性质得AH=HE=1,接着利用勾股定理可计算出DH=$\sqrt{15}$,再证明四边形DHQC为矩形得CQ=DH=$\sqrt{15}$,HQ=CD=4,∠HQC=90°,然后在Rt△ACQ中利用勾股定理计算出AC=2$\sqrt{10}$,从而可得PQ=$\frac{\sqrt{10}}{3}$.
解答 解:作DH⊥AB于H,CQ⊥AB于Q,如图,
∵四边形ABCD为菱形,
∴AD=AB=CD=4,CD∥AB,
∵E、F分别是AB、CD中点,
∴DF=BE=2,
而DF∥BE,
∴四边形DEBF为平行四边形,
∴PM=PQ,DE∥BF,
∴ME为△ABQ的中位线,
∴AM=MQ,
同理可得CQ=MQ,
∴AM=MQ=CQ,
∴PQ=$\frac{1}{6}$AC,
∵AD=DE=4,DH⊥AE,
∴AH=HE=1,
∴DH=$\sqrt{A{D}^{2}-A{H}^{2}}$=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$,
∵CD∥HQ,DH∥CQ,
∴四边形DHQC为平行四边形,
而∠DHQ=90°,
∴四边形DHQC为矩形,
∴CQ=DH=$\sqrt{15}$,HQ=CD=4,∠HQC=90°,
在Rt△ACQ中,AC=$\sqrt{C{Q}^{2}+A{Q}^{2}}$=$\sqrt{(\sqrt{15})^{2}+{5}^{2}}$=2$\sqrt{10}$,
∴PQ=$\frac{1}{6}$×2$\sqrt{10}$=$\frac{\sqrt{10}}{3}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了平行四边形的判定与性质和勾股定理.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 直线y=-x上 | B. | 直线y=x上 | C. | 双曲线y=$\frac{1}{x}$ | D. | 抛物线y=x2上 |
| A. | 2的立方根是8 | |
| B. | 36的立方根是27 | |
| C. | 一个正数或负数的立方根与这个数同号,0的立方根是0 | |
| D. | 如果一个数的立方根等于它本身,那么这个数只是1或0 |
| A. |  | B. |  | C. |  | D. |  |
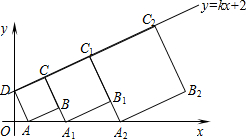 在平面直角坐标系中,直线y=kx+2与y轴交于点D,点A的坐标为(1,0),以AD为边作正方形ABCD.点C在直线y=kx+2上,延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形(即正方形ABCD)的面积为5.第2014个正方形的面积为5×$(\frac{9}{4})^{2014}$.
在平面直角坐标系中,直线y=kx+2与y轴交于点D,点A的坐标为(1,0),以AD为边作正方形ABCD.点C在直线y=kx+2上,延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形(即正方形ABCD)的面积为5.第2014个正方形的面积为5×$(\frac{9}{4})^{2014}$.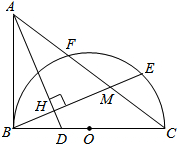 如图,已知△ABC,以BC为直径,O为圆心的半圆交AC于点E,点E为弧CF的中点,连接BE交AC于点M,AD为△ABC的角平分线交BC于点D,且AD⊥BE,垂足为点H
如图,已知△ABC,以BC为直径,O为圆心的半圆交AC于点E,点E为弧CF的中点,连接BE交AC于点M,AD为△ABC的角平分线交BC于点D,且AD⊥BE,垂足为点H 如图,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得C点的俯角为β,则较低建筑物CD的高度为?
如图,两建筑物的水平距离为a米,从A点测得D点的俯角为α,测得C点的俯角为β,则较低建筑物CD的高度为? 如图,⊙O是△ABC的外接圆,若∠ABC=60°,则∠CAO等于30°.
如图,⊙O是△ABC的外接圆,若∠ABC=60°,则∠CAO等于30°.