题目内容
17.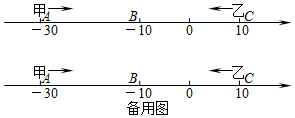 已知数轴上有A,B,C三点,分别代表-30,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A,B,C三点,分别代表-30,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A、B、C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
分析 (1)设x秒后甲与乙相遇,根据甲与乙的路程和为40,可列出方程求解即可;
(2)设y秒后甲到A,B,C三点的距离之和为48个单位,分甲应为于AB或BC之间两种情况讨论即可求解:
(3)设z秒后甲与乙在数轴上相遇,需要分类讨论:①若甲从A向右运动3秒时返回;②若甲从A向右运动7秒时返回,分别表示出甲、乙表示的数,结合线段间的和差关系列出方程并解答.
解答 解:(1)设x秒后,甲、乙在数轴上相遇.
则4x+6x=40,解得x=4,
-30+4×4=-14
答:甲,乙在数轴上表示-14的点相遇.
(2)能.显然,当甲在点C右侧时,甲到A,B,C的距离和大于40+20=60,
故甲应运动到AB或BC之间.
设y秒后,甲到A,B,C的距离和为48个单位.
当甲在AB之间时:4y+(20-4y)+(40-4y)=48,
解得y=3;
当甲在BC之间时:4y+(4y-20)+(40-4y)=48,
解得x=7;
答:3或7秒后,甲到A,B,C的距离和为48个单位.
(3)设甲调头z秒后与乙相遇.
若甲从A向右运动3秒时返回,
甲表示的数为:-30+4×3-4z;乙表示的数为:10-6×3-6z,
由题意得:-30+4×3-4z=10-6×3-6z,
解得z=5.
相遇点表示的数为:-30+4×3-4×5=-38.
若甲从A向右运动7秒时返回,
甲表示的数为:-30+4×7-4z;乙表示的数为:10-6×7-6z,
依据题意得:-30+4×7-4z=10-6×7-6z,
解得z=-15(舍去).
(注:此时甲在表示-2的点上,乙在表示-32的点上,乙在甲的左侧,甲追及不上乙,因而不可能相遇.)
答:甲从A向右运动3秒时返回,甲,乙能在数轴上相遇,相遇点表示的数为-38.
点评 此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题在解答第(2)、(3)问注意分类思想的运用.

| A. | 3x2-x2=3 | B. | 3a2+2a2=5a4 | C. | -0.25ab+$\frac{1}{4}$ab=0 | D. | 3+x=3x |
 如图,点P是等边△ABC外一点,PA=3,PB=4,PC=5
如图,点P是等边△ABC外一点,PA=3,PB=4,PC=5




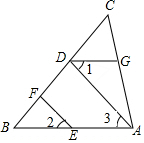 如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数.
如图,EF⊥BC,AD⊥BC,∠1=∠2,∠B=30°.求∠GDB的度数. 已知:如图所示,AB=AC,CE与BF相交于点D,且BD=CD.求证:DE=DF.
已知:如图所示,AB=AC,CE与BF相交于点D,且BD=CD.求证:DE=DF. 已知:△ABC.
已知:△ABC.