题目内容
7. 如图,点P是等边△ABC外一点,PA=3,PB=4,PC=5
如图,点P是等边△ABC外一点,PA=3,PB=4,PC=5(1)将△APC绕点A逆时针旋转60°得到△P1AC1,画出旋转后的图形;
(2)在(1)的图形中,求∠APB的度数.
分析 (1)将△APC绕点A逆时针旋转60°得到△P1AC1如图所示.
(2)只要证明△APP1是等边三角形,由PB2+PP12=P1B2,推出∠P1PB=90°,即可解决问题.
解答 解:(1)将△APC绕点A逆时针旋转60°得到△P1AC1,如图所示,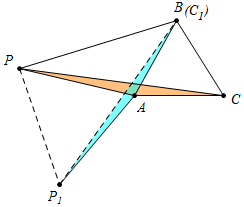
(2)∵△AP1C1是由△APC旋转所得,
∴△AP1C1≌△APC,
∴P1C1=PC=5,AP=AP1=3,∠PAP1=60°,
∴△APP1是等边三角形,
∴PP1=AP=3,∠APP1=60°,
∵PB=4,P1B=5,PP1=3,
∴PB2+PP12=P1B2,
∴∠P1PB=90°
∴∠APB=∠BPP1-∠APP1=30°.
点评 本题考查等边三角形的性质、旋转变换、勾股定理的逆定理、全等三角形的判定和性质等知识,解题的关键是学会利用旋转变换添加辅助线,构造全等三角形,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
18. 有理数a、b在数轴上的位里如图所示,则下列结论中正确的是( )
有理数a、b在数轴上的位里如图所示,则下列结论中正确的是( )
 有理数a、b在数轴上的位里如图所示,则下列结论中正确的是( )
有理数a、b在数轴上的位里如图所示,则下列结论中正确的是( )| A. | a+b>0 | B. | a-b<0 | C. | ab>0 | D. | a÷b>0 |
15.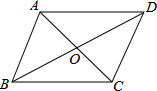 如图,已知四边形ABCD是平行四边形,对角线相交于点O,要使它成为矩形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,对角线相交于点O,要使它成为矩形,那么需要添加的条件可以是( )
 如图,已知四边形ABCD是平行四边形,对角线相交于点O,要使它成为矩形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,对角线相交于点O,要使它成为矩形,那么需要添加的条件可以是( )| A. | AB=BC | B. | AB=AC | C. | AC=BD | D. | AC⊥BD |
2.抛物线y=-$\frac{1}{2}$x2向左平移1个单位长度得到抛物线的解析式为( )
| A. | y=-$\frac{1}{2}$x(x+1)2 | B. | y=-$\frac{1}{2}$x(x-1)2 | C. | y=-$\frac{1}{2}$x2+1 | D. | y=-$\frac{1}{2}$x2-1 |
19.等腰三角形的两边为5和6,则三角形的周长是( )
| A. | 16或17 | B. | 16或11 | C. | 16 | D. | 17 |

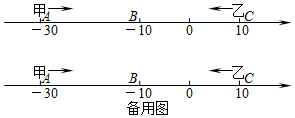 已知数轴上有A,B,C三点,分别代表-30,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A,B,C三点,分别代表-30,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.