题目内容
8.若$a=-{({\frac{1}{3}})^{-2}}$,$b={({-\frac{1}{3}})^2}$,c=0.32,则下列四式中正确的是( )| A. | a<c<b | B. | b<a<c | C. | c<a<b | D. | a<b<c |
分析 首先根据负整指数幂的运算方法、有理数的乘方的运算方法,分别求出a、b、c的值各是多少;然后根据实数大小比较的方法判断出它们的大小关系即可.
解答 解:$a=-{({\frac{1}{3}})^{-2}}$=-9,$b={({-\frac{1}{3}})^2}$=$\frac{1}{9}$,c=0.32=0.09,
∵-9$<0.09<\frac{1}{9}$,
∴a<c<b.
故选:A.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了有理数的乘方问题,要熟练掌握,解答此题的关键是要明确:有理数的乘方运算与有理数的加减乘除运算一样,首先要确定幂的符号,然后再计算幂的绝对值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列多项式中,能够因式分解的是( )
| A. | a2+b2 | B. | p2-6p+9 | C. | x2-xy+y2 | D. | -m2-n2 |
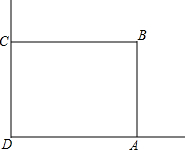 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角AD,DC(两强足够长)用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,若围成的花园面积为192m2,求x的值.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角AD,DC(两强足够长)用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,若围成的花园面积为192m2,求x的值. 如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?
如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?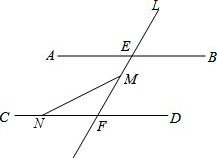 如图,AB∥CD,点M是线段EF上一点,若点N是直线CD上的一个动点(点N不与F重合)
如图,AB∥CD,点M是线段EF上一点,若点N是直线CD上的一个动点(点N不与F重合)