题目内容
5.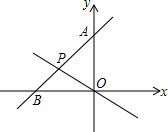 如图,已知直线y=x+6的图象与x轴、y轴交于A、B两点.
如图,已知直线y=x+6的图象与x轴、y轴交于A、B两点.(1)求点A、点B的坐标和△AOB的面积.
(2)求线段AB的长.
(3)若直线l经过原点,与线段AB交于点P(P为一动点),把△AOB的面积分成2:1两部分,求直线L的解析式.
分析 (1)把x=0,和y=0代入解析式y=x+6解答即可,再利用三角形的面积公式计算即可;
(2)利用两点间的距离公式计算即可;
(3)设P点的坐标为(m,m+6),然后分两种情况求得P的坐标,进而利用待定系数法即可求得直线L的解析式.
解答 解:(1)∵直线y=x+6的图象与x轴、y轴交于A、B两点,
∴A(0,6)B(-6,0),
∴OA=6,OB=6,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×6×6=18;
(2)∵A(0,6)B(-6,0),
∴AB=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$;
(3)设P点的坐标为(m,m+6),
∴S△POB=$\frac{1}{2}$OB•(m+6)=3(m+6),
∵把△AOB的面积分成2:1两部分,
∴S△POB:S△AOB=2:3或1:3,
∴$\frac{3(m+6)}{18}$=$\frac{2}{3}$或$\frac{1}{3}$,
解得m=-2或-4,
∴P(-2,4)或(-4,2),
设直线L的解析式为y=kx,
∴4=-2k或2=-4k,
解得k=-2或k=-$\frac{1}{2}$,
∴直线L的解析式为$y=-\frac{1}{2}x$或y=-2x.
点评 本题考查了两条直线相交问题,三角形的面积问题,待定系数法求一次函数的解析式,注意(3)中P的坐标是两种情况.

练习册系列答案
相关题目
9.下列各组数中,互为相反数的是( )
| A. | 5和-$\frac{1}{5}$ | B. | 2与-2 | C. | -1与-1 | D. | 0.01与|-0.01| |
16.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为( )
| A. | 2×106 | B. | 2×107 | C. | 2×10-6 | D. | 2×10-7 |
14.下列说法正确的是( )
| A. | (2xy)2的系数是2 | B. | (ab)3的次数是6次 | ||
| C. | $\frac{x+y}{5}$是单项式 | D. | x2-x的常数项不存在 |
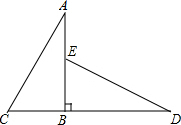 如图,已知AB⊥CD,垂足为B,AB=DB,AC=DE.请你判断∠D与∠A的关系,并说明理由.
如图,已知AB⊥CD,垂足为B,AB=DB,AC=DE.请你判断∠D与∠A的关系,并说明理由.