题目内容
13.分解因式(ab+1)2-(a+b)2=(a+1)(b+1)(a-1)(b-1);多项式x2+y2-6x+8y+7的最小值为-18.分析 先利用平方差公式分解,再利用分组分解法分解即可;
将多项式x2+y2-6x+8y+7配成(x-3)2+(y+4)2-18的形式,然后根据完全平方式的非负性即可解答.
解答 解:(ab+1)2-(a+b)2
=(ab+1+a+b)(ab+1-a-b)
=(a+1)(b+1)(a-1)(b-1);
x2+y2-6x+8y+7=(x-3)2+(y+4)2-18≥-18,
当且仅当x=3,y=-4时等号成立,
所以多项式x2+y2-6x+8y+7的最小值为-18.
故答案为:(a+1)(b+1)(a-1)(b-1);-18.
点评 此题主要考查因式分解的应用,非负数偶次方的性质,是基础题,熟记平方差公式与完全平方公式是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
3.抛物线y=2x2+4x-1的顶点关于原点对称的点的坐标是( )
| A. | (-1,3) | B. | (-1,-3) | C. | (1,3) | D. | (1,-3) |
 如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..
如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..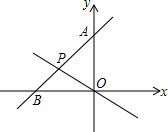 如图,已知直线y=x+6的图象与x轴、y轴交于A、B两点.
如图,已知直线y=x+6的图象与x轴、y轴交于A、B两点.