题目内容
17.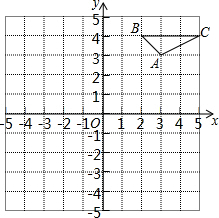 如图,在平面直角坐标系中△ABC三个顶点分别为A(3,3)、B(2,4)、C(5,4).
如图,在平面直角坐标系中△ABC三个顶点分别为A(3,3)、B(2,4)、C(5,4).(1)将△ABC平移后,点A的对应点A1的坐标为(2,-2),请画出平移后的△A1B1C1.
(2)将△A1B1C1绕点O顺时针旋转90°,得到△A2B2C2,请画出旋转后的△A2B2C2.在这个旋转过程中,点B1所经过的路径长为$\frac{\sqrt{2}}{2}$π.
分析 (1)利用平移的性质得出各点位置进而得出答案;
(2)利用旋转的性质得出对应点位置进而得出答案,再利用弧长公式求出即可.
解答  解:(1)如图所示:△A1B1C1即为所求;
解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
点B1所经过的路径长为:$\frac{90π×\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
故答案为:$\frac{\sqrt{2}}{2}$π.
点评 此题主要考查了平移变换以及旋转变换,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
6.不等式-2x<-6的解集是( )
| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |

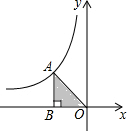 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过点A向x轴做垂线,垂足为B,若△ABO的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过点A向x轴做垂线,垂足为B,若△ABO的面积为6,则k的值为( )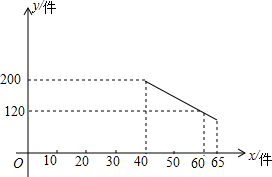 某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(40≤x≤65)时,每月的销售量y(件)与销售单价x(元)之间满足如图所示的一次函数关系.
某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(40≤x≤65)时,每月的销售量y(件)与销售单价x(元)之间满足如图所示的一次函数关系.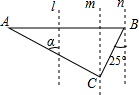 如图,直线l∥m∥n,直角△ABC的直角顶点C在直线m上,顶点B在直线n上,边BC与直线n所夹锐角为25°,则∠a的度数为65°.
如图,直线l∥m∥n,直角△ABC的直角顶点C在直线m上,顶点B在直线n上,边BC与直线n所夹锐角为25°,则∠a的度数为65°.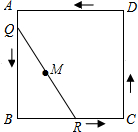 如图,有一条长度为1的线段QR,其端点Q、R在边长为1的正方形ABCD的四边上滑动一周时,QR的中点M所经过的路线长为π.
如图,有一条长度为1的线段QR,其端点Q、R在边长为1的正方形ABCD的四边上滑动一周时,QR的中点M所经过的路线长为π.