题目内容
2.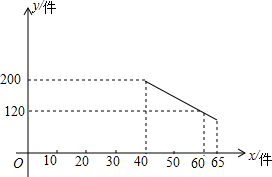 某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(40≤x≤65)时,每月的销售量y(件)与销售单价x(元)之间满足如图所示的一次函数关系.
某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(40≤x≤65)时,每月的销售量y(件)与销售单价x(元)之间满足如图所示的一次函数关系.(1)求y与x的函数关系式;
(2)设每月获得的利润为P(元),求P与x之间的函数关系式;
(3)若想每月获得1600元的利润,那么销售单价应定为多少元?
(4)当销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
分析 (1)设y与x的函数关系式为:y=kx+b(k≠0),将(40,200),(60,120)代入,利用待定系数法即可求出一次函数解析式;
(2)根据由题意得,p与x的函数关系式为:p=(x-40)(-4x+360);
(3)再利用当P=2400时,解方程求出x的值即可;
(4)根据(2)的函数关系式,利用求二次函数最值的方法便可解出答案.
解答 解:(1)解(1)设y与x的函数关系式为:y=kx+b(k≠0),
由题意得
$\left\{\begin{array}{l}{40k+b=200}\\{60k+b=120}\end{array}\right.$,
解得
$\left\{\begin{array}{l}{k=-4}\\{b=360}\end{array}\right.$.
故y=-4x+360(40≤x≤65);
(2)由题意得,p与x的函数关系式为:
p=(x-40)(-4x+360)=-4x2+520x-14400,
(3)当P=1600时,
-4x2+520x-14400=1600,
解得:x1=50,x2=80(不合题意舍去),
故销售单价应定为50元.
(4)由题意得,p与x的函数关系式为:
p=(x-40)(-4x+360)=-4x2+520x-14400=-4(x-65)2+2500,
当x=65元时,最大利润是2500元.
点评 此题考查了一次函数与二次函数的应用,根据已知图象上点的坐标得出直线解析式是解题关键掌握待定系数法是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
12.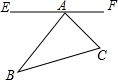 如图,图中与∠C是同旁内角的角有几个( )
如图,图中与∠C是同旁内角的角有几个( )
 如图,图中与∠C是同旁内角的角有几个( )
如图,图中与∠C是同旁内角的角有几个( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.五一小长假期间,某景区接待游客约为630000人,将数据630000用科学记数法表示为( )
| A. | 63×103 | B. | 6.3×103 | C. | 6.3×104 | D. | 6.3×105 |
11.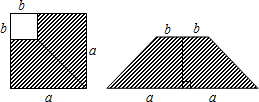 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )
在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形(如图),通过计算阴影部分的面积,验证了一个等式,这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab-b2 | D. | a2-ab=a(a-b) |
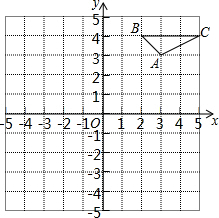 如图,在平面直角坐标系中△ABC三个顶点分别为A(3,3)、B(2,4)、C(5,4).
如图,在平面直角坐标系中△ABC三个顶点分别为A(3,3)、B(2,4)、C(5,4).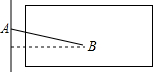 如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离大于4.6米.(填“大于”“小于”或“等于”)
如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离大于4.6米.(填“大于”“小于”或“等于”) 李老师为锻炼身体一直坚持步行上下班,一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来说了半小时的话,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间t(分)之间的关系.
李老师为锻炼身体一直坚持步行上下班,一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来说了半小时的话,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间t(分)之间的关系. 由三个形状完全相同的菱形组成一个正六边形.只用无刻度的直尺按下列要求画图.
由三个形状完全相同的菱形组成一个正六边形.只用无刻度的直尺按下列要求画图.