题目内容
12. 如图,已知O为三边垂直平分线交点,∠BAC=60°,则∠BOC=120°.
如图,已知O为三边垂直平分线交点,∠BAC=60°,则∠BOC=120°.
分析 由点O为三边垂直平分线交点,得到点O为△ABC的外心,根据同弧所对的圆周角等于圆心角的一半即可得到结果.
解答 解:∵已知点O为三边垂直平分线交点,
∴点O为△ABC的外心,
∴∠BOC=2∠BAC,
∵∠BAC=60°,
∴∠BOC=120°,
故答案为:120°.
点评 本题考查了线段垂直平分线的性质,三角形的外心的性质,解答本题关键熟练掌握圆周中同一弧线所对应的圆周角是圆心角的一半.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.一列数a1,a2,a3,…an,其中a1=-1,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$,则a2014=( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 2014 |
1.若已知分式$\frac{|m|-2}{m-2}$的值为0,则m的值为( )
| A. | ±2 | B. | 2 | C. | 0 | D. | -2 |
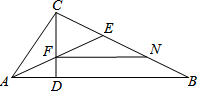 如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是①②③④.
如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是①②③④. 如图,已知在等腰△ABC中,∠A=∠B=30°过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°过点C作CD⊥AC交AB于点D.