��Ŀ����
10����֪�ı���ABCD������A��B������ֱ�Ϊ��m��0������n��0����������C���ڷ�����������ͼ���ϣ����dz��������ı���Ϊ�������ı���ABCD��������C��Ϊ���������㡱��С���Դ�����dz�����Ȥ���Է���������Ϊy=$\frac{2}{x}$ʱ���������̽����
��1���������ı���ABCDΪ������ʱ��С�����ֲ���mȡ��ֵ��������������������������ֻ����������һ�������εĶ���C�ڵ�һ���ޣ���һ�������εĶ���C1�ڵ������ޣ�
����ͼ1��ʾ����A������Ϊ��1��0����ͼ���ѻ�������������һ������������ABCD����֪��������C������Ϊ��2��1�������㻭����һ������������AB1C1D1����д����������C1������Ϊ��-1��-2����
��С��ͨ���ı��A�����꣬��ֱ��CC1�Ľ���ʽy��kx+b������̽�����ɵ�k��1��b���ú�m��ʽ�ӱ�ʾ����-m��
��2���������ı���ABCDΪ���Σ������ڱߵı�Ϊ1��2����A������Ϊ��2��0���������������C�����꣮
���� ��1�����������ε����ʺ͡������ı���ABCD���Ķ���������ͼ�Σ��ó�����C1�����ꣻ
��������ó���C��C1�����꣬����y��kx+b���ó������飬�ⷽ���鼴�ɣ�
��2��������������ٵ�AB=2BCʱ���ɵ�A������ó���C������Ϊ$��n\;��\;\frac{n-2}{2}��$��$��{n\;��\;\frac{2-n}{2}}��$����������ó����̣��ⷽ�̼��ɣ�
�ڵ�BC=2ABʱ��������ó���C������Ϊ��n��2n-4����n��4-2n������������ó����̣��ⷽ�̼��ɣ�
��� �⣺��1������ͼ1��ʾ����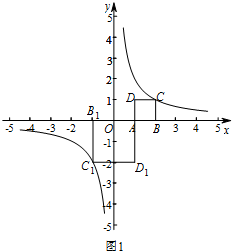 C1������Ϊ��-1��-2����
C1��������-1��-2����
�ʴ�Ϊ����-1��-2����
��������ã�C������Ϊ��n��n-m����C1������Ϊ��m-n��-n����
����y��kx+b�ã�$\left\{\begin{array}{l}{nk+b=n-m}\\{��m-n��k+b=-n}\end{array}\right.$��
��ã�k=1��b=-m��
�ʴ�Ϊ��1��-m��
��2��������������ٵ�AB=2BCʱ��
�ߵ�A������Ϊ��2��0����
���C������Ϊ$��n\;��\;\frac{n-2}{2}��$��$��{n\;��\;\frac{2-n}{2}}��$��
��$n��\frac{n-2}{2}=2$��$n��\frac{2-n}{2}=2$��
��ã�$n=1��\sqrt{5}$����ʵ����
���C������Ϊ$��{1+\sqrt{5}\;��\frac{{\sqrt{5}-1}}{2}}��$��$��{1-\sqrt{5}\;��\;\frac{{-\sqrt{5}-1}}{2}}��$��
�ڵ�BC=2ABʱ��
��C��������n��2n-4����n��4-2n����
��n��2n-4��=2��n��4-2n��=2��
��ã�$n=1��\sqrt{2}$��n=1��
���C������Ϊ$��{1+\sqrt{2}\;��\;2\sqrt{2}-2}��$��$��{1-\sqrt{2}\;��\;-2-2\sqrt{2}}��$��1��2����
������������C������Ϊ$��{1+\sqrt{5}\;��\frac{{\sqrt{5}-1}}{2}}��$��$��{1-\sqrt{5}\;��\;\frac{{-\sqrt{5}-1}}{2}}��$��$��{1+\sqrt{2}\;��\;2\sqrt{2}-2}��$��$��{1-\sqrt{2}\;��\;-2-2\sqrt{2}}��$��1��2����
���� �����Ƿ����������ۺ���Ŀ�������ˡ������ı���ABCD�������ʡ���������������ʽ�����á�һ�κ�������ʽ���������ε����ʣ����ε����ʡ����̵Ľⷨ��֪ʶ�������ۺ���ǿ����һ���Ѷȣ����⡰�����ı���ABCD���ǽ������Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | $\frac{2+a}{{-4-4a-{a^2}}}$ | B�� | $\frac{a-b}{b-a}$ | C�� | $\frac{{{x^2}-4}}{x-2}$ | D�� | $\frac{{{x^2}+{y^2}}}{x+y}$ |
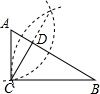
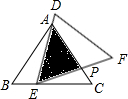 ��ͼ���ڡ�ABC�У���֪AB=AC=6��BC=8���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����P�㣮
��ͼ���ڡ�ABC�У���֪AB=AC=6��BC=8���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����P�㣮
 ��?ABCD�У���E��F�ֱ���AB��CD�ϣ���AE=CF����֤��DE=BF��
��?ABCD�У���E��F�ֱ���AB��CD�ϣ���AE=CF����֤��DE=BF��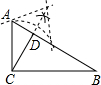


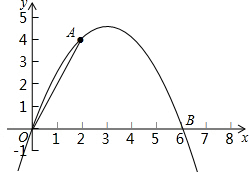 ��ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0����
��ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0����