题目内容
8.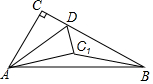 如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3.
如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3.
分析 分两种情况进行讨论:当点C1在AB上时,△BDC1为直角三角形;当∠ADC=45°时,△BDC1为直角三角形,分别根据含30°角的直角三角形的性质以及勾股定理进行计算即可.
解答 解:如图所示,当点C1在AB上时,∠AC1D=∠C=90°,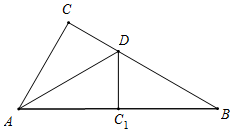
∴∠BC1D=90°,即△BDC1为直角三角形,
∵∠ABC=30°,AB=6,
∴AC=$\frac{1}{2}$AB=3,BD1=2DC1=2CD,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3$\sqrt{3}$,
∴BD=$\frac{2}{3}$BC=2$\sqrt{3}$;
如图所示,当∠ADC=45°时,∠CDC1=90°,此时△BDC1为直角三角形,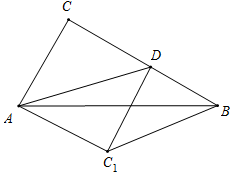
∵∠C=90°,
∴△ACD是等腰直角三角形,
∴CD=AC=3,
而BC=3$\sqrt{3}$,
∴BD=BC-CD=3$\sqrt{3}$-3.
故答案为:2$\sqrt{3}$或3$\sqrt{3}$-3.
点评 本题主要考查了折叠问题以及含30°角的直角三角形的性质的运用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;翻折变换(折叠问题)实质上就是轴对称变换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.要锻造直径为2厘米,高为16厘米的圆柱形机器零件10件,则需直径为4厘米的圆钢柱长( )
| A. | 10厘米 | B. | 20厘米 | C. | 30厘米 | D. | 40厘米 |
19.一正方形面积为27,则它的边长为( )
| A. | 在3到4之间 | B. | 在4到5之间 | C. | 在5到6之间 | D. | 在6到7之间 |
3.某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为3200元和4000元.
(1)若某工厂每月支付的工人工资为440000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,填写下表,并列方程求解.
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
(1)若某工厂每月支付的工人工资为440000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,填写下表,并列方程求解.
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
| 工种 | 工人每月工资(元) | 招聘人数 | 工厂应付工人的约工资(元) |
| A | 3200 | x | 3200x |
| B | 4000 | 120-x | 4000(120-x) |
20.如果一次函数y=kx+b的函数值y随x的增大而减小,且与y轴正半轴相交,那么( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
18.若式子$\frac{\sqrt{3-x}}{3x+2}$有意义,则x的取值范围是( )
| A. | x≤3 | B. | x≥-$\frac{2}{3}$且x≠3 | C. | x≠-$\frac{2}{3}$ | D. | x≤3且x≠-$\frac{2}{3}$ |
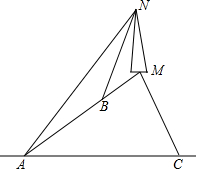 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求: