题目内容
20. 如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.
如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.(1)求a的值和点B的坐标;
(2)设抛物线的顶点是P,试求△PAB的面积;
(3)在抛物线上是否存在点M,使得△MAB的面积等于△PAB的面积的2倍?若存在,求出点M的坐标.
分析 (1)利用待定系数法即可解决问题.
(2)先求出顶点P坐标,即可解决问题.
(3)由S△MAB=$\frac{1}{2}$×4×|yM|=2 S△PAB=8,推出|yM|=4,∴yM=±4,再列出方程即可解决问题.
解答 解:(1)将(-3,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=-$\frac{1}{2}$;
∵抛物线对称轴方程为x=-1,A、B两点关于对称轴对称,
∴B的坐标为(1,0),
(2)∵y=-$\frac{1}{2}$(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=XB-XA=1-(-3)=4,
∴S△PAB=$\frac{1}{2}$×4×2=4.
(3)S△MAB=$\frac{1}{2}$×4×|yM|=2 S△PAB=8
∴|yM|=4,∴yM=±4,
当yM=4时,y=-$\frac{1}{2}$(x+1)2+2=4,无解.
当yM=-4时,y=-$\frac{1}{2}$(x+1)2+2=-4,
解得x=-1±2$\sqrt{3}$
∴M(-1+2$\sqrt{3}$,-4)或M(-1-2$\sqrt{3}$,-4)
点评 本题考查抛物线与x轴的交点,三角形的面积等知识,解题的关键是熟练掌握待定系数法,确定函数解析式,学会构建方程解决实际问题,属于中考常考题型.

练习册系列答案
相关题目
8. 将如图中的图形折叠起来围成一个正方体,可以得到( )
将如图中的图形折叠起来围成一个正方体,可以得到( )
 将如图中的图形折叠起来围成一个正方体,可以得到( )
将如图中的图形折叠起来围成一个正方体,可以得到( )| A. |  | B. |  | C. |  | D. |  |
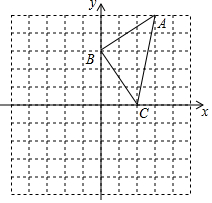 (1)在如图所示的直角坐标系中,有一个三角形△ABC.把△ABC向下平移6个单位,得到△A1B1C1,再作△A1B1C1关于y轴的对称图形△A2B2C2,请在直角坐标系中画出△A1B1C1与△A2B2C2.
(1)在如图所示的直角坐标系中,有一个三角形△ABC.把△ABC向下平移6个单位,得到△A1B1C1,再作△A1B1C1关于y轴的对称图形△A2B2C2,请在直角坐标系中画出△A1B1C1与△A2B2C2.