题目内容
1.已知y与x-2成正比例,且x=3时,y=-2.(1)求出y与x的函数关系式.
(2)在平面直角坐标系中画出(1)中函数的大致图象.
(3)求此函数图象与两坐标轴围成的三角形面积.
分析 (1)设y与x的关系式为y=k(x-2),把x=3,y=-2代入求出k值即可得出y与x的关系式;
(2)求出一次函数与两坐标轴的交点,画出直线即可.
(3)根据一次函数与两坐标轴的交点,即可求出三角形的面积.
解答 解:(1)设y与x的关系式为y=k(x-2),
把x=3,y=-2代入解析式得k(3-2)=-2,
解得k=-2.
故函数解析式为y=-2x+4;
(2)当y=0,则0=-2x+4,解得:x=2,则直线与x轴的交点坐标为:(2,0),
当x=0,则y=4,则直线与y轴的交点坐标为:(0,4),如图所示:
(3)此函数图象与两坐标轴围成的三角形面积=$\frac{1}{2}$×2×4=4.
点评 本题考查的是用待定系数法求一次函数的关系式,在解答此类问题时要注意利用一次函数的性质,列出方程组,求出k值,从而求得其解析式.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
6.某班30名同学在“献爱心”活动中都捐赠了图书,各人捐赠的本数如下5,2,4,5,3,2,4,3,5,4,3,4,2,3,3,4,4,5,3,4,3,5,3,5,3,4,3,4,3,3.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
(1)填写全班同学捐书册数统计表中未完成的部分.
(2)画出扇形统计图,描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比.
| 捐书册数 | 划记 | 人数 | 百分比 |
| 2 |  | 3 | 10% |
| 3 | 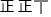 | 12 | 40% |
| 4 | 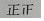 | 9 | 30% |
| 5 |  | 6 | 20% |
13.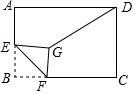 如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )
如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )
 如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )
如图,在矩形ABCD中,AB=6,AD=8,E是AB的中点,点F是BC边上的动点,将△EBF沿EF所在的直线折叠到△EGF的位置,连接GD,则GD的最小值是( )| A. | $\sqrt{73}-3$ | B. | $\sqrt{34}$ | C. | 6 | D. | $\frac{32}{5}$ |
10. 如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
 如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )
如图,△ABC与△DEF是位似图形,点A(-1,2)和点D(2,-4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为( )| A. | (2m,2n) | B. | (-2m,-2n) | C. | (2m,-2n) | D. | (-2m,2n) |
11.下列式子为最简二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{\frac{1}{2}}$ |
 如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.
如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.