题目内容
13. 如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
分析 延长ED交BC于F,根据平行线的性质求出∠MFC=∠B=70°,求出∠FDC=40°,根据三角形外角性质得出∠C=∠MFC-∠MDC,代入求出即可.
解答 解:
延长ED交BC于F,
∵AB∥DE,∠ABC=70°,
∴∠MFC=∠B=70°,
∵∠CDE=140°,
∴∠FDC=180°-140°=40°,
∴∠C=∠MFC-∠MDC=70°-40°=30°,
故选B.
点评 本题考查了三角形外角性质,平行线的性质的应用,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
4.一个多边形的每个内角都等于120°,则这个多边形的边数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
1.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | x2•x3=x6 | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | (x2)3=x6 |
8.已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是( )
| A. | m=-1 | B. | m=3 | C. | m≤-1 | D. | m≥-1 |
2.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
则这四人中发挥最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
13.|-2+3×(-2)|=( )
| A. | -8 | B. | 2 | C. | 4 | D. | 8 |
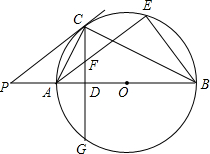 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.