题目内容
 甲、乙两车分别从A、B两地沿直线同时匀速前往C地,最终到达C地(A、B、C三地顺次在同一直线上).设甲、乙两车行驶x(时)后,与B地相距的距离分别为y1(千米)和y2(千米),y1、y2与x的函数关系如图.
甲、乙两车分别从A、B两地沿直线同时匀速前往C地,最终到达C地(A、B、C三地顺次在同一直线上).设甲、乙两车行驶x(时)后,与B地相距的距离分别为y1(千米)和y2(千米),y1、y2与x的函数关系如图.(1)A、B两地距离为
(2)点P的坐标为
(3)两车行驶几小时,甲车遇到乙车?
考点:一次函数的应用
专题:
分析:(1)根据题意,甲开始时的距离即为A、B两地间的距离;
(2)求出0≤x≤0.5时甲的函数解析式,乙的解析式然后联立求解即可,再根据y值相等解答;
(3)利用追及问题的等量关系列出方程求解即可.
(2)求出0≤x≤0.5时甲的函数解析式,乙的解析式然后联立求解即可,再根据y值相等解答;
(3)利用追及问题的等量关系列出方程求解即可.
解答:解:(1)由图可知,A、B两地距离为50千米;
(2)0≤x≤0.5时,甲:设函数解析式为y=kx+b,
则
,
解得
,
所以,y=-100x+50,
乙:设函数解析式为y=kx,
则5k=400,
解得k=80,
所以,y=80x,
联立
,
解得
,
所以,P(
,
),
点P的实际意义:甲、乙两车行驶
小时,甲、乙两车距B地距离相等均为
千米,乙车在甲车前面;
故答案为:(1)50千米;(2)(
,
),甲、乙两车行驶
小时,甲、乙两车距B地距离相等均为
千米,乙车在甲车前面;
(3)设经x小时,甲车遇到乙车,
由题意得,100x-80x=50,
解得x=2.5.
答:甲车行驶2.5小时遇到乙车.
(2)0≤x≤0.5时,甲:设函数解析式为y=kx+b,
则
|
解得
|
所以,y=-100x+50,
乙:设函数解析式为y=kx,
则5k=400,
解得k=80,
所以,y=80x,
联立
|
解得
|
所以,P(
| 5 |
| 18 |
| 200 |
| 9 |
点P的实际意义:甲、乙两车行驶
| 5 |
| 18 |
| 200 |
| 9 |
故答案为:(1)50千米;(2)(
| 5 |
| 18 |
| 200 |
| 9 |
| 5 |
| 18 |
| 200 |
| 9 |
(3)设经x小时,甲车遇到乙车,
由题意得,100x-80x=50,
解得x=2.5.
答:甲车行驶2.5小时遇到乙车.
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,联立两函数解析式求交点坐标,追及问题,读懂题目信息并准确识图获取信息是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四个数中绝对值最小的数是( )
| A、0 | ||
| B、-2 | ||
C、-
| ||
D、
|
 一束光线经3块平面镜反射,反射的路线如图所示,图中字母表示相应的度数,已知c=60°,求d+e与x的值.
一束光线经3块平面镜反射,反射的路线如图所示,图中字母表示相应的度数,已知c=60°,求d+e与x的值. 在正方形ABCD中,E是CD上一点,AF⊥AE交CB的延长线于点F,连接DF,分别交AE、AB于点G、P.若∠BAF=∠BFD,证明四边形APED是矩形.
在正方形ABCD中,E是CD上一点,AF⊥AE交CB的延长线于点F,连接DF,分别交AE、AB于点G、P.若∠BAF=∠BFD,证明四边形APED是矩形.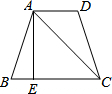 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点A作AE⊥BC,垂足为点E,∠B=60°,∠CAD=45°,AC=4
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点A作AE⊥BC,垂足为点E,∠B=60°,∠CAD=45°,AC=4 如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.