题目内容
6.先化简,再求代数式(1-$\frac{3}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$的值,其中x是不等式组$\left\{\begin{array}{l}{2(x+2)<3x+2}\\{\frac{x}{3}≤\frac{x+1}{4}}\end{array}\right.$的整数解.分析 首先将括号里面进行通分运算,进而利用分式除法运算法则化简,再解不等式组得出不等式组的整数解,进而代入求出答案.
解答 解:原式=$\frac{x+2-3}{x+2}$×$\frac{x+2}{(x-1)(x+1)}$
=$\frac{1}{x+1}$,
$\left\{\begin{array}{l}{2(x+2)<3x+2①}\\{\frac{x}{3}≤\frac{x+1}{4}②}\end{array}\right.$
解不等式①得:x>2,
解不等式②得:x≤3,
故不等式组的解集是:2<x≤3,
故不等式组的整数解为:3,
当x=3时,原式=$\frac{1}{3+1}$=$\frac{1}{4}$.
点评 此题主要考查了分式的化简求值以及不等式组的解法,正确进行分式的混合运算是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
14.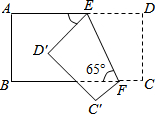 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )
 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠C′FB等于( )| A. | 70° | B. | 65° | C. | 50° | D. | 25° |
15. 实数a在数轴上的位置如图所示,则a的值可能为( )
实数a在数轴上的位置如图所示,则a的值可能为( )
 实数a在数轴上的位置如图所示,则a的值可能为( )
实数a在数轴上的位置如图所示,则a的值可能为( )| A. | -4 | B. | -3 | C. | -2 | D. | 1 |
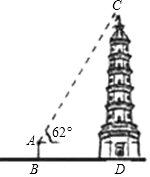 如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图所示,位于昆明市昙华市内的瑞应塔,被誉为云南第一塔,某校九年级数学课外活动小组的同学准备利用假期测量超然楼的高度,甲同学在距离塔底部25m的B处地塔顶C的仰角为62°,若甲同学的眼睛到地面的高度AB为176cm,求瑞应塔C的高度(结果精确到0.1m,参考数据sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)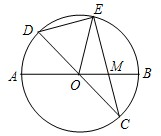 已知:如图,在半径我4的⊙O中,AB、CD是两条直径,M我OB的中点,CM的延长线交⊙O于点E,且EM>MC,连接DE,DE=$\sqrt{15}$.
已知:如图,在半径我4的⊙O中,AB、CD是两条直径,M我OB的中点,CM的延长线交⊙O于点E,且EM>MC,连接DE,DE=$\sqrt{15}$.