题目内容
9. 如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是65°.
如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是65°.
分析 先根据平行线的性质得∠2=∠1=120°,然后根据三角形外角性质计算∠ACB的大小.
解答  解:∵l∥m,
解:∵l∥m,
∴∠2=∠1=120°,
∵∠2=∠ACB+∠A,
∴∠ACB=120°-55°=65°.
故答案为65°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
4.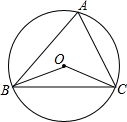 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )| A. | 22° | B. | 26° | C. | 32° | D. | 68° |
18.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
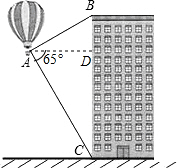 如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可) 小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?
小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?