题目内容
10.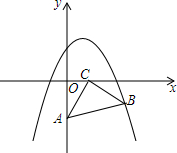 在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.
在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.(1)以AC为直角边的等腰三角形还能画3个,请画出来.
(2)求点B的坐标;
(3)求抛物线的解析式;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
分析 (1)根据等腰直角三角形的定义,可得答案;
(2)根据全等三角形的判定与性质,可得CD、BD的长,可得B点坐标;
(3)根据待定系数法,可得函数解析式;
(4)根据线段中点的坐标,可得P1点坐标,根据全等三角形的判定与性质,可得P2,P3点坐标,根据点的坐标是否满足函数解析式,可得答案.
解答 解:(1)以AC为直角边的等腰三角形还能画3个,如图1: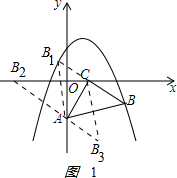
(2)如图2,作BD⊥OC于D点,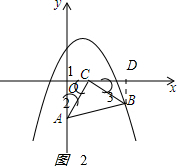
∵等腰直角三角板ABC,
∴AC=BC,∠ACB=90°,
∴∠1+∠3=90°.
∵∠1+∠2=90°,
∴∠2=∠3.
在△AOC和△CDB中,
$\left\{\begin{array}{l}{∠1=∠3}\\{∠AOC=∠CDB}\\{AC=BC}\end{array}\right.$,
∴△AOC≌△CDB (AAS),
∴CD=AO=2,BD=OC=1.
∵D=OD+CD═1+2=3,
∴B点坐标为(3,-1);
(3)将B点坐标代入函数解析式,得
9a-3a+2=-1,
解得a=-$\frac{1}{2}$,
抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2;
(3)如图3,作P3D⊥OA于D点,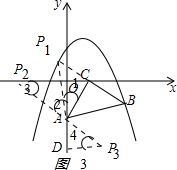 ,
,
P1、B关于C点对称,
P1的横坐标为=2×1-3=-1,纵坐标为0-(-1)=1,即P1(-1,1),
当x=-1时,y=-$\frac{1}{2}$+$\frac{1}{2}$×(-1)+2=1,P1在抛物线上;
∠1+∠2=90°,∠2+∠3=90°,
∠1=∠3.
在△AP2O和△COA中,
$\left\{\begin{array}{l}{∠3=∠1}\\{∠AO{P}_{2}=∠COA}\\{A{P}_{2}=AO}\end{array}\right.$,
∴△AP2O≌△COA (AAS),
P2O=AO=2,
P2(-2,0),
当x=-2时,-$\frac{1}{2}$×(-2)2+$\frac{1}{2}$×(-2)+2=-1,
B2不在抛物线上;
由△P3DA≌△P2OA,得
P3D=P2O=2,AD=AC=2,
OD=AD+AO=4,
即P3(2,-4),
当x=2时,-$\frac{1}{2}$×22+$\frac{1}{2}$×2+2=1,
P3不在抛物线上;
综上所述:在抛物线上在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形,P(-1,1).
点评 本题考查了二次函数综合题,利用了等腰直角三角形的定义,全等三角形的判定与性质是求B点坐标的关键;利用待定系数法求函数解析式;利用全等三角形的判定与性质求出P点坐标,再把P点坐标代入函数解析式检验是解题关键.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| 成绩 | 10.7 | 10.8 | 10.9 | 11.0 | 11.2 |
| 次数 | 3 | 3 | 1 | 2 | 1 |
(2)试求该名运动员10次百米赛跑的平均成绩是多少?
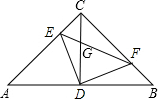 如图,CD是等腰直角△ABC斜边上的高,E是AC上任意一点,DF⊥DE,交BC于F点.
如图,CD是等腰直角△ABC斜边上的高,E是AC上任意一点,DF⊥DE,交BC于F点. 已知a、b所表示的数如图所示,下列结论正确的有②;(只填序号)
已知a、b所表示的数如图所示,下列结论正确的有②;(只填序号)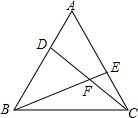 如图,在等边三角形ABC中,D、E分别为AB、BC边上的两点,且AD=CE,求证:∠EBA=∠DCB.
如图,在等边三角形ABC中,D、E分别为AB、BC边上的两点,且AD=CE,求证:∠EBA=∠DCB.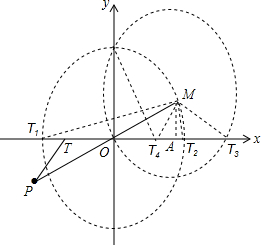 如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.
如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.