题目内容
16.化简或计算:(1)|$\sqrt{2}-\sqrt{3}$|+$\sqrt{3}(\sqrt{3}+\frac{\sqrt{2}}{\sqrt{3}})$;
(2)$\root{3}{1-\frac{19}{27}}+\root{3}{\frac{7}{8}-1}$.
分析 (1)原式利用绝对值的代数意义,以及二次根式乘法法则计算即可得到结果;
(2)原式整理后,利用立方根定义计算即可得到结果.
解答 解:(1)原式=$\sqrt{3}$-$\sqrt{2}$+3+$\sqrt{2}$=$\sqrt{3}$+3;
(2)原式=$\root{3}{\frac{8}{27}}$+$\root{3}{-\frac{1}{8}}$=$\frac{2}{3}$-$\frac{1}{2}$=$\frac{1}{6}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
4. 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )| A. | -1 | B. | 1 | C. | 1-2a | D. | 2a-1 |
11. 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )
 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )| A. | AC=BD | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
8.若a<b,则下列各式中不正确的是( )
| A. | a+3<b+3 | B. | a-3<b-3 | C. | -3a<-3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
5.如图所示的是四个物理实验工具的简图,从左到右依次是小车、弹簧、钩码、三极管,其中是轴对称图形的是( )
| A. | 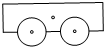 小车 | B. |  弹簧 | C. |  钩码 | D. | 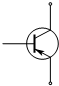 三极管 |
18.已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且0<y-x<1,则k的取值范围是( )
| A. | -1$<k<-\frac{1}{2}$ | B. | 0$<k<\frac{1}{2}$ | C. | 0<k<1 | D. | $\frac{1}{2}$<k<1 |
 如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.
如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.